A Single GNN Layer

하나의 GNN Layer에서는 vector set을 하나의 vector로 compress한다. 이를 위해 2가지 과정이 필요한데, 첫째는 Message Transformation, 두번째는 Message Aggregation이다.

Message Transformation(Computation)

Message Transformation 단계에서는 Message function을 사용하여 노드의 임베딩을 메시지로 바꾼다.

\(m_{u}^{(l)} = MSG^{(l)}(h_{u}^{(l-1)})\)

예를들어 메시지 함수를 \(W^{(l)}\)과 같은 matrix를 곱하는 방식으로 적용할 수 있다.

Message Aggregation

Message Aggregation은 메시지를 aggregation을 통해 임베딩으로 바꾸는 것이다.

\(h_{v}^{(l)} = AGG^{(l)}({m_{u}^{(l)},u \in N(v)})\)

이때 Aggregation function으로는 Sum, Mean, Max 등이 사용될 수 있다.

Putting things together

위의 내용에 추가로 \(h_{v}^{(l)}\)이 \(h_{v}^{(l-1)}\)의 정보를 받을 수 있도록 추가해주고, 이를 별도의 weight를 곱해 새로운 메시지를 구한다.

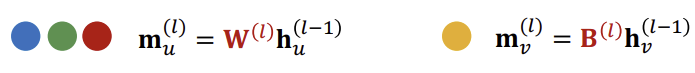
이후 이웃들로부터의 aggregation이 끝난 후, 두 메시지를 concat(혹은 summation)하여 임베딩을 만든다.

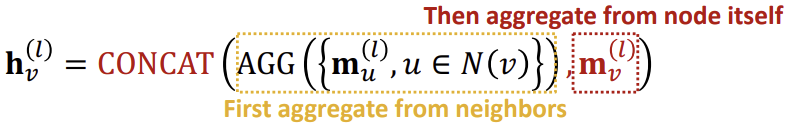
여기에 ReLu, Sigmoid와 같은 non-linear 활성화 함수를 곱해주면 GNN의 한 layer에 대한 수식이 완성된다.

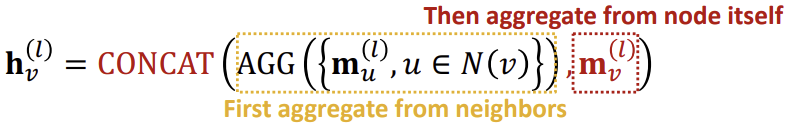
Classical GNN Layers : GCN(Graph Convolutional Network)

다른 GNN 기반의 모델들 또한 기본적으로 Message Transformation과 Message Aggregation의 구성을 갖추고 있다.

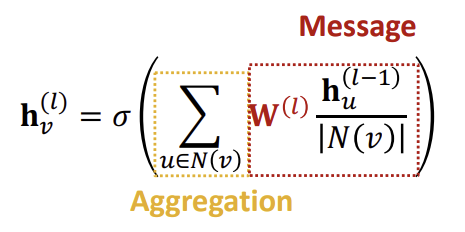
GCN의 경우, 위 그림에서 노란색 부분이 Aggregation, 빨간색 부분이 Message Transformation이다.

Message Transformation 부분에서는 Node의 degree로 Neighbor의 Embedding을 Normalize하여 사용하는 것을 알 수 있고, Aggregation 부분에서는 Sum을 활용하는 것을 확인할 수 있다. 이후 마지막으로 활성화 함수를 추가한 것이 GCN의 한 Layer의 계산법이다.

Classical GNN Layers : GraphSAGE

GraphSAGE 또한 Message 파트와 Aggregation 파트로 나눌 수 있다.

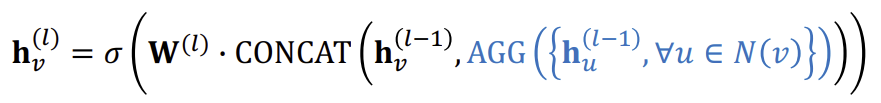
위 그림에서 Message 파트는 2개의 stage로 나눌 수 있다. 첫번째 stage는 \(AGG()\)로 표현된 부분으로, \(h_{u}^{(l-1)}\)을 aggregation하여 \(h_{N(v)}^{(l)}\)을 구하는 부분이고, 두번째 stage는 이전에 구한 \(h_{N(v)}^{(l)}\)와 \(h_{v}^{(l-1)}\)을 concat하여 \(h_{v}^{(l)}\)을 구하는 부분이다.

Aggregation 과정에서는 Mean, MLP를 이용한 Pool, LSTM등의 방식들이 사용될 수 있다.

마지막으로 GraphSAGE는 L2 normalization을 매 Layer마다 사용해서 모든 임베딩 벡터의 유클리드 길이를 1로 만드는 과정을 포함하고 있다.

Classical GNN Layers : GAT

GAT에는 GCN과 GraphSAGE에는 없었던 Attention weight(\(\alpha\))이 존재한다. 이전 GAT와 GCN에서는 \(\alpha_{vu}\)가 \(1/\vert N(v) \vert)이었다면, GAT에서는 각 이웃들에 대한 중요도를 모두 동일하게 적용하지 않는다.

그렇다면 이러한 \(\alpha_{vu}\)는 어떻게 구해야할까?

먼저 Attention mechanism \(a\)를 이용해 attention coefficient \(e_{vu}\)를 구한다. 이때의 \(e_{vu}\)는 \(u\)에서 \(v\)로 향하는 메시지에 대한 중요도이고, attention score는 방향에 대해 symmetric하지 않을 수 있다.

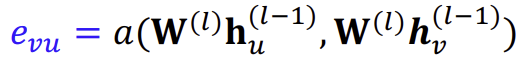
이후 softmax를 이용하여 모든 이웃에 대한 \(e_{vu}\)의 합이 1이 되도록 normalize하면 최종적인 \(\alpha_{vu}\)가 된다. 이를 통해 weighted sum으로 최종 attention weight \(\alpha_{vu}\)를 계산한다.

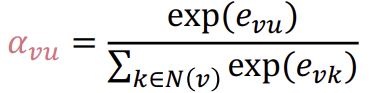
그렇다면 Attention mechanism \(a\)는 뭘까?

Attention mechanism \(a\)는 아래의 그림과 같이 두 노드의 임베딩을 계산을 통해 weight \(e\)로 만든다.

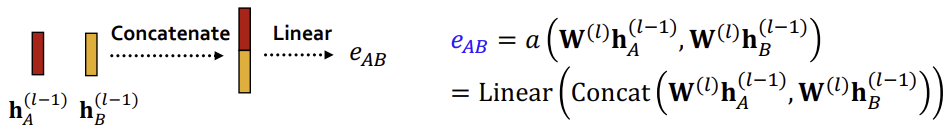
그리고 \(W^{(l)}\)과 같은 다른 weight matrix들과 같이 파라미터 학습을 통해 개선된다.

Multi-head Attention

추가로, 어텐션은 학습시키거나 converge 시키기가 어려울 수 있다. 이를 해결하기 위해 multi-head attention을 사용하는 방식이 존재한다. multi-head attention은 한 edge에 대한 attention score(weight)를 여러개 만들어서 simultanious하게 학습시키는 방식을 의미한다. 여러개의 weight들은 각각 local minima에 converge 되고, 이를 평균내는 방식을 통해 모델을 robust하게 만들 수 있다.

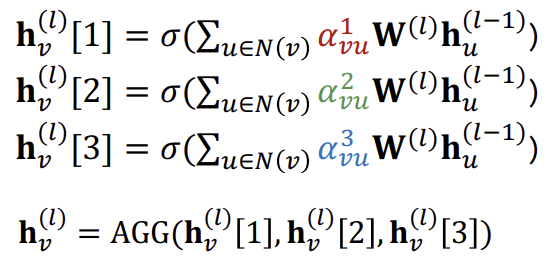
Attention Mechanism의 장점

Attention Mechanism은 이웃들에게 각기 다른 중요도를 부여하여 모델을 세밀하게 할 수 있다. 또한 병렬적으로 연산이 가능해 computationally 효율적이다. Non-zero element를 많이 포함하지 않고, 그래프의 크기와 무관하게 고정된 수의 파라미터를 가져 storgae 또한 효율적이다.

GNN Layer in Practice

실제로 GNN을 설계할 때는 여러 Deep Neural Network 모듈들을 GNN에서도 사용할 수 있다. 아래는 그런 모듈들에 대한 예시이다.

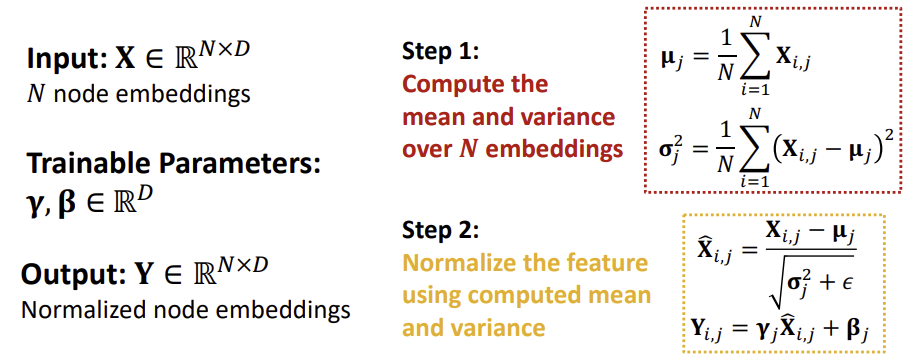
Batch Normalization

Batch Normalization은 Node 임베딩을 평균을 0, 분산을 1로 만들기 위한 방법으로, 임베딩에서 평균을 빼고 표준편차로 나누는 방식으로 진행된다. 이러한 Batch Normalization은 Neural Network의 training 과정을 안정화할 수 있다는 장점이 있다.

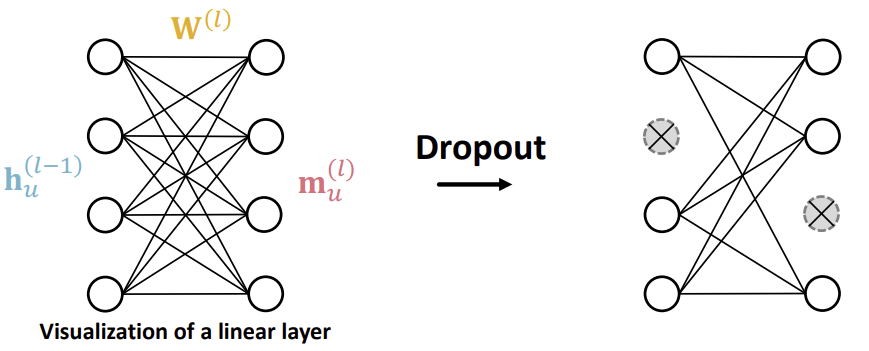
Dropout

Dropout은 overfitting을 방지하기 위해 사용되는 방법으로, 학습 과정에서 메시지 함수의 linear layer에서 input과 output을 일정 비율로 무시한다. 단, test set에서는 Dropout을 진행하지 않는다.

Activation(Non-linearity)

이러한 Deep Learning의 모듈들의 활용을 통해 퍼포먼스가 더 좋은 GNN layer를 만들 수 있다.

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 7.2 - A Single Layer of a GNN