Machine Learning as Optimization

GNN에 본격적으로 들어가기 전, 우선 Deep Learning에 대해 간단하게 복습해보고자 한다.

우리가 진행할 ML의 목표는 supervised learning으로, input \(x\)를 받고, label \(y\)를 예측하는 것이다. 그리고 이를 공식으로 표현하면 아래와 같다.

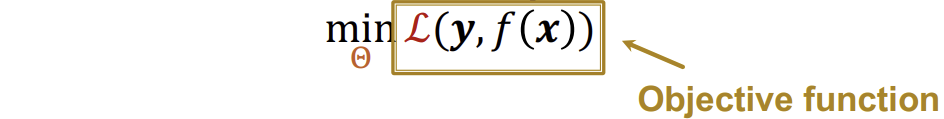
이때, 함수 \(f(x)\)는 input \(x\)를 넣었을 때, label \(y\)를 예측하는 함수이고, \(y\)는 실제 label의 값이다. \(\theta\)는 우리가 optimize하는 parameter의 set이고, \(L\)은 Loss function을 의미한다(ex. L1, L2, cross entropy 등).

따라서 위 식이 의미하는 바는, \(\theta\)를 조정해가며, \(y\)(실제값)와 \(f(x)\)(예측값)의 차이를 최소화하는 것이 ML의 목표라는 것이다.

그렇다면 최적의 \(\theta\)를 어떻게 찾을 수 있을까?

이때, Gradient vector를 사용한다.

Gradient Descent

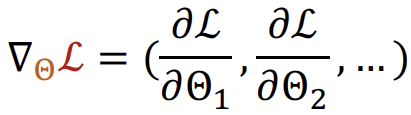
\(\theta\)의 component들인 \(\theta_1\), \(\theta_2\) 등을 각각 미분한 합으로 multi-variable function인 loss function \(L\)의 변화량을 구하는 것이다. 이를 통해 가장 크게 증가하는 방향을 찾을 수 있다.

Gradient Descent는 이를 iterative하게 진행하여, gradient의 반대방향으로 (Loss가 감소하는 방향으로) weight를 업데이트 하는 알고리즘이다.

그 과정에서 하이퍼파라미터 Learning rate(LR) \(\eta\)는 gradient step을 결정하고, 이상적으로는 gradient가 0일 때 알고리즘이 종료해야하지만, 실제로는 validation set에서 더 이상 결과가 좋아지지 않는 경우 알고리즘이 끝난다.

Stochastic Gradient Descent (SGD)

이러한 Gradient Descent에는 한가지 문제점이 존재한다. \(\nabla_{\theta}L(y, f(x))\)에서 매번 gradient를 계산할 때마다 전체 dataset인 \(x\)를 계산해서 합해야 한다는 것이다.

이러한 문제의 해결법이 Stochastic gradient descent(SGD)이다.

Stochastic gradient descent는 매 step마다 dataset의 subset인 minibatch \(B\)를 선정하여 input \(x\)로 사용한다.

아래는 SGD에서 사용하는 용어들이다.

• Batch size : minibatch에 들어가는 data point의 수
• Iteration : 한 minibatch의 SGD 1 step
• Epoch : 전체 dataset에 대해 Iteration을 진행한 것 (dataset size / batch size 횟수만큼 iteration을 진행함)

이러한 SGD는 convergence가 보장되지 않아 learning rate 튜닝이 필요하다. SGD는 가장 기본적인 idea이며, Adam, Adagrad 등 SGD를 기반으로 발전시킨 다양한 알고리즘들이 존재한다.

Neural Network Function

먼저 앞에서 살펴보았던 Objective를 토대로 함수 \(f\)를 linear function으로 가정하여 살펴보자. 만약 \(f\)의 결과가 스칼라 형태라면 \(W\)는 벡터 형태일 것이고, \(f\)의 결과가 벡터 형태라면 \(W\)는 weight matrix 형태일 것이다.

그렇다면 \(f(x)\)가 더 복잡한 형태라면 어떨까?

이땐 위와같이 chain rule을 이용하여 Back-propagation을 수행하여 \(\theta\)에 대한 \(L\)의 gradient를 구할 수 있다.

아래는 2계층의 linear network에 대한 예시이다.

위 예시에서 \(h(x) = W_{1}x\)로 hidden layer를 두어 \(f(x) = W_{2}h(x))로 계산을 하고있다.

Non-linearity

하지만 \(f(x) = W_{2}(W_{1}x)\)에서 \(W_{2}W_{1}\)은 또 하나의 matrix 형태이기 때문에 아무리 많은 weight matrix를 결합해도 \(f(x)\)는 linear하게 된다.

이를 개선하기 위해 ReLU, Sigmoid 등의 non-linear한 함수들을 결합하여 다양한 형태의 함수를 표현할 수 있도록 한다.

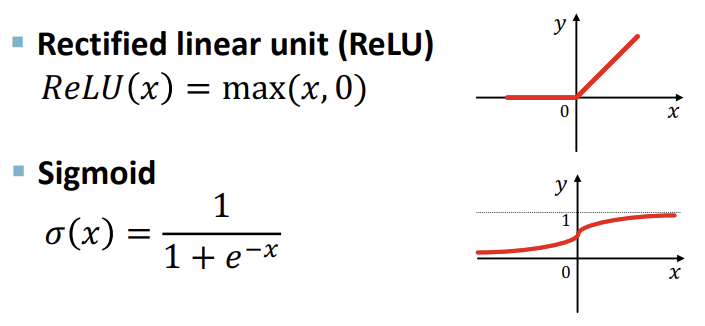
이러한 non-linear 함수, 즉 활성화 함수를 결합하여 다층 Neural Network를 형성한 것이 Multi-layer Perceptron(MLP)이다.

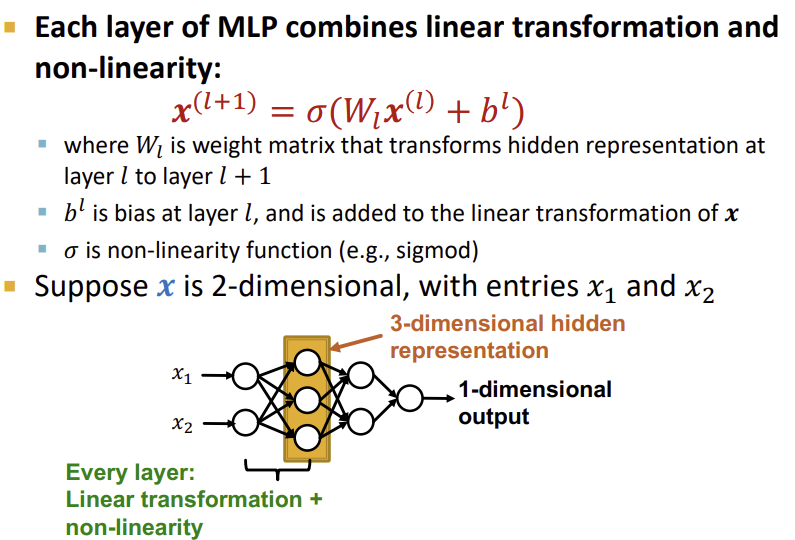
위의 예시에서와 같이 기본적인 Neural Network의 함수에 bias를 더하고, 이를 non-linear 함수로 묶어서 식을 만들면, 이를 여러 계층을 통과시켰을 때 모든 형태의 함수를 표현 가능하게 되는 것이다.

Summary

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 6.2 - Basics of Deep Learning