Components of a Network

Graph는 Object, Interacion, System으로 구성되어있다. 부르는 명칭은 조금씩 차이날 수 있으나 의미는 같다.

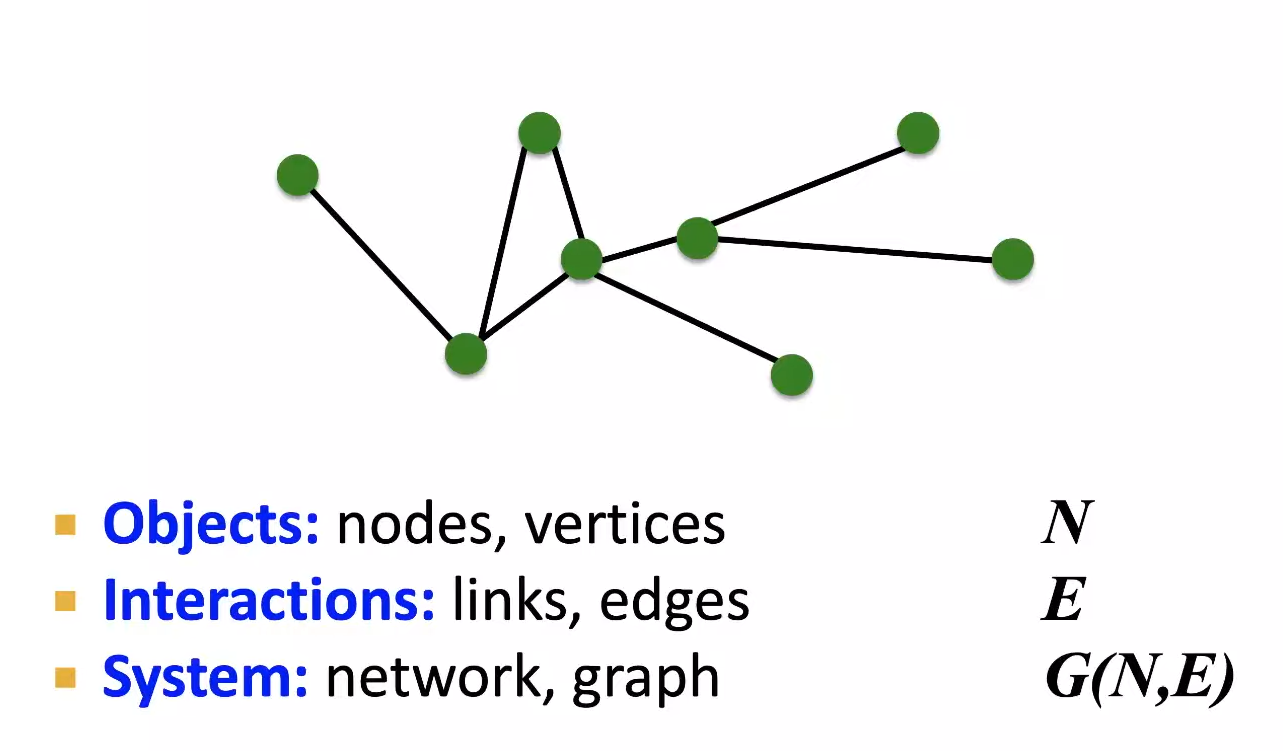
Graph는 Common Language로, 다양한 종류의 관계를 Graph로 표현할 수 있다. 따라서 Graph를 이용한 머신러닝에서는 주어진 도메인에서 Node와 Edge를 무엇으로 설정하느냐에 따라 모델의 목적이 정해지고 성공 여부가 결정된다.

이번 글에서는 Graph의 여러 종류와 그를 표현하는 방법론에 대해 알아보고자 한다.

Directed/Undirected Graph

Graph의 종류들 중 첫번째로 알아볼 것은 Directed/Undirected Graph이다. 둘은 Node의 차이는 없지만 Link에 방향성이 없고 대칭적인지, 혹은 방향성이 존재하는지에 따라 나뉜다.

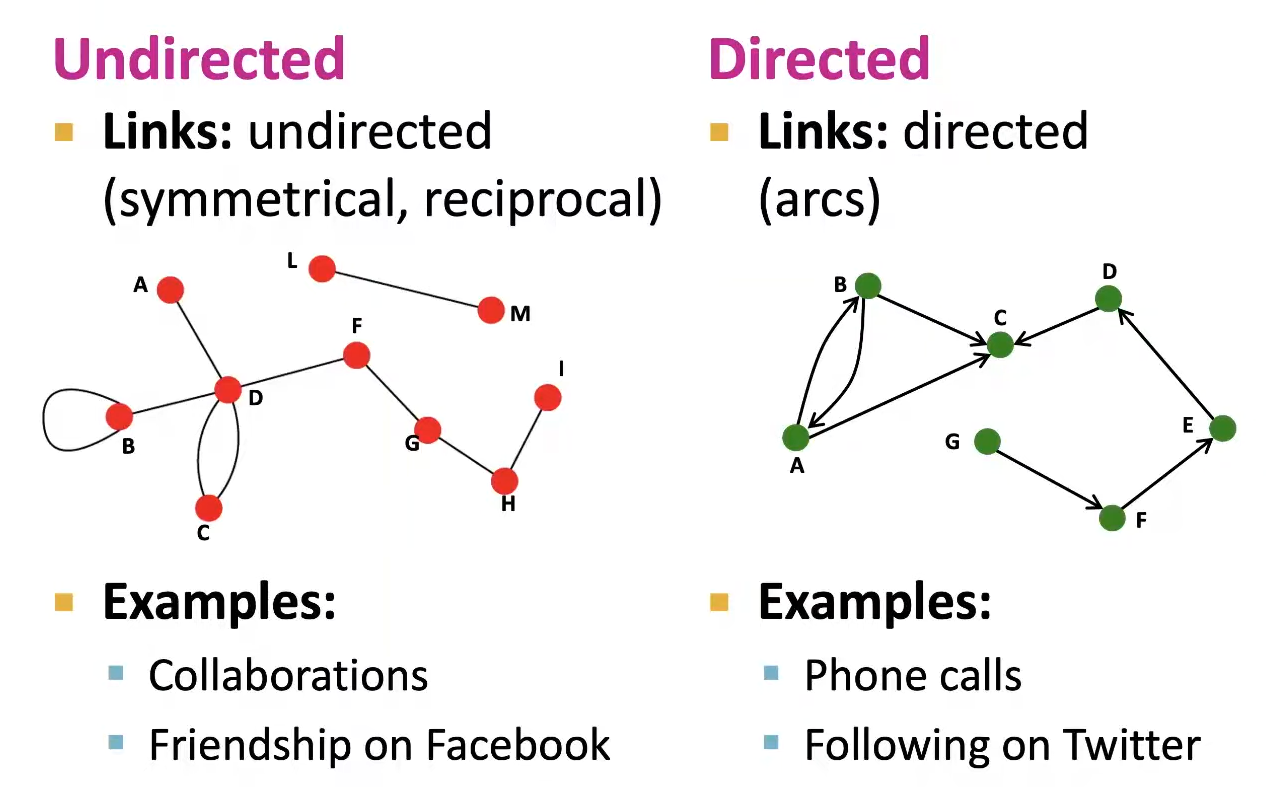
추가적으로, Undirected Graph의 경우 Node Degree는 인접한 node의 개수를 의미한다. 단, self-edge(loop)가 있는 경우에는 degree가 2 증가한다. 반면 Directed Graph의 경우, in-degree와 out-degree로 구분하여 계산한다.

Connected/Disconnected Graph

Connected Graph와 Disconnected Graph는 Connected Component의 개수로 구분할 수 있다. Connected Component는 연결되어있는 Node들의 집합으로, Connected Graph는 1개의, Disconnected Graph는 2개 이상의 Connected Component로 이루어져있다.

재미있게도 Disconnected된 Component들은 행렬에서 같은 행 또는 열을 공유하지 않고 대각에 위치한 Block의 형태로 표현된다.

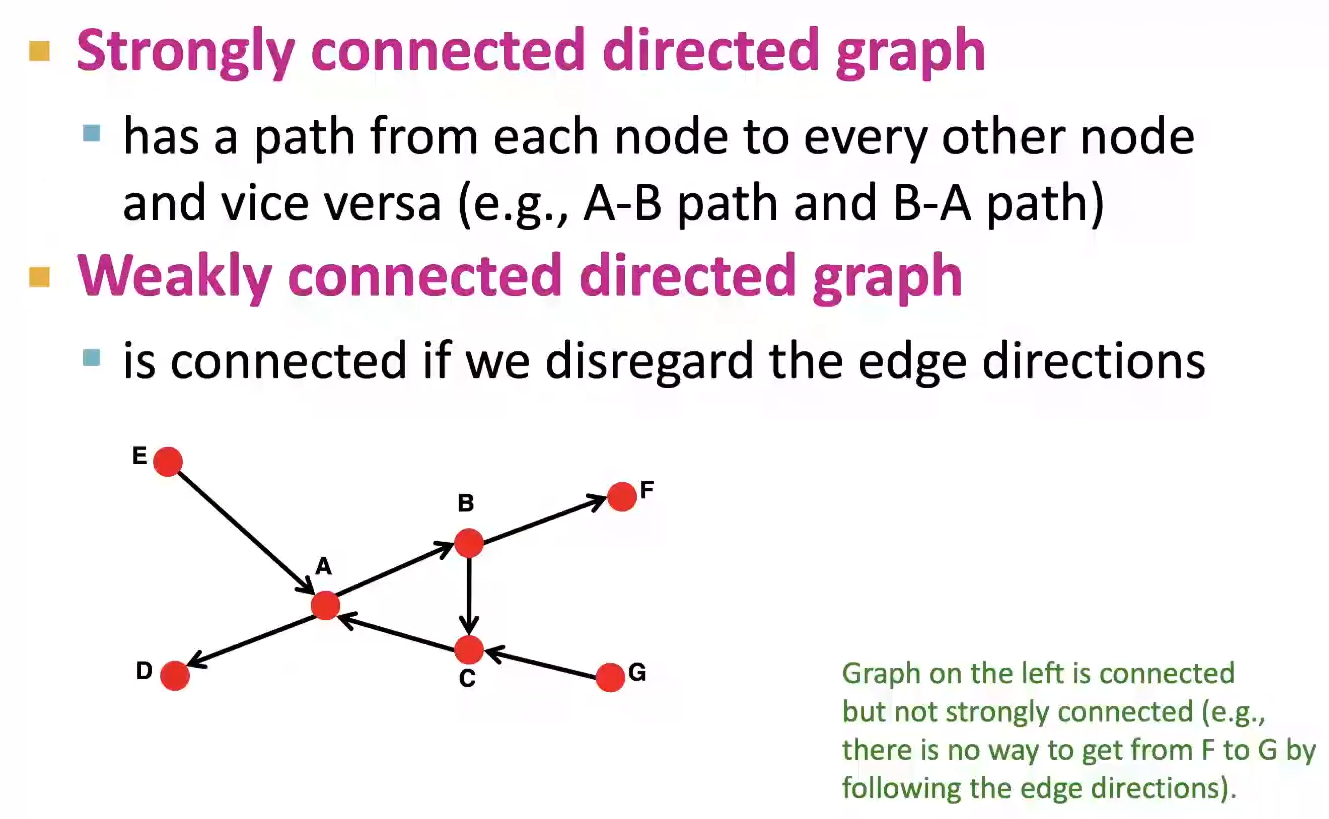
만약 Graph가 Directed Graph인 경우, 방향과 무관하게 모든 Node들이 연결되어있기만 하다면 Weakly Connected Directed Graph로 정의하고, 방향성을 고려하여 Graph를 이루는 각 Node에서 다른 모든 Node로 갈 수 있는 길이 존재한다면, Strongly Connected Directed Graph로 정의한다.

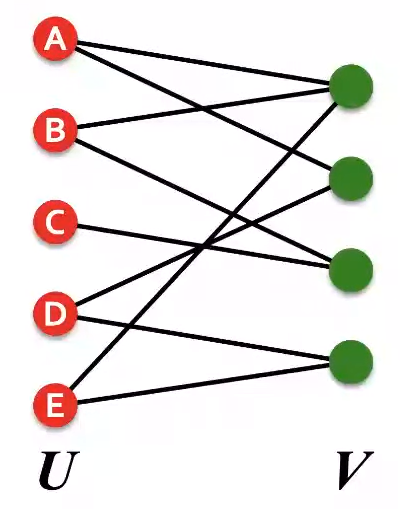
Bipartite Graph

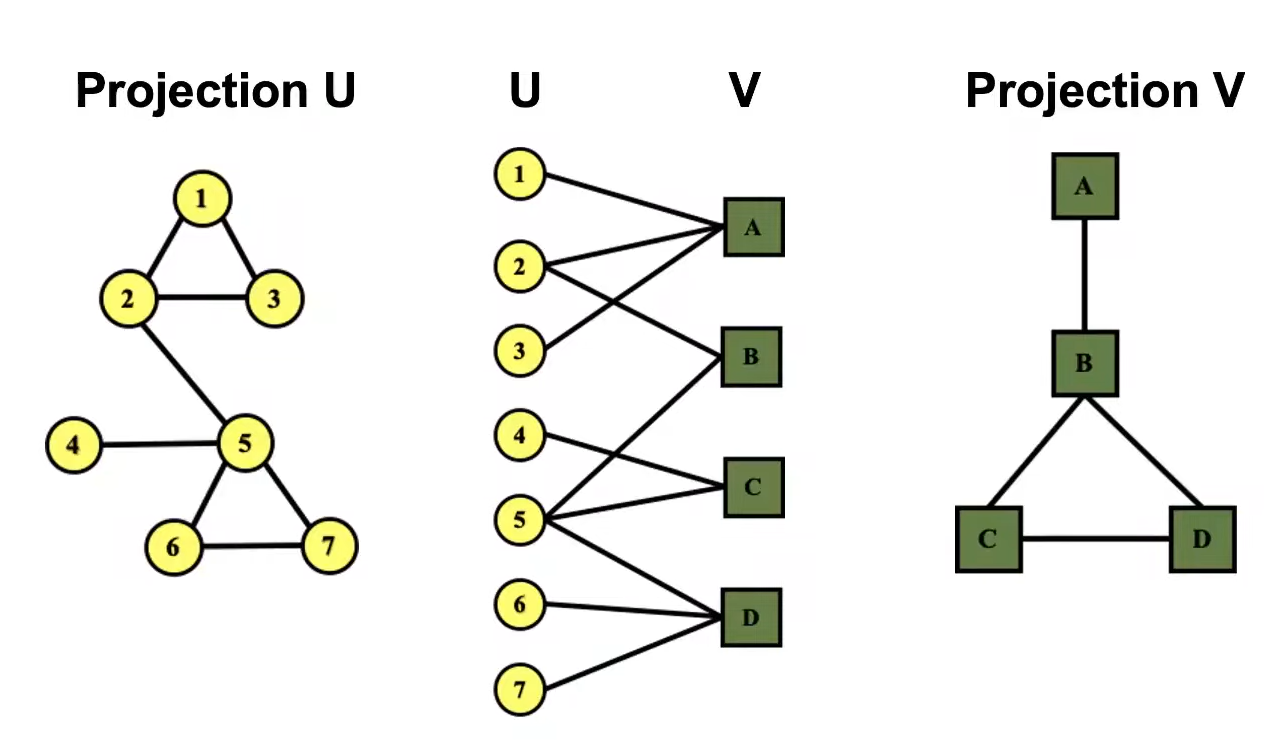
Bipartite Graph는 Node의 종류가 2개인 그래프를 의미한다. (2개 이상인 경우 Multipartite라고 한다.) 단, 이때 Edge는 종류가 다른 Node들 사이만을 연결한다. 예를들어 논문과 저자, 영화와 배우의 관계를 표현할 때 사용할 수 있다.

Bipartite Graph는 Folded Network 형태로 표현 또한 가능한데, 이는 Node들 중 한 종류만 표현하여, 해당 Node들이 공통된 Node와의 Node를 지니고 있다면 그들 사이에 Edge를 그린다. 에를 들어 같은 논문에 이름이 실린 저자, 혹은 같은 영화에 출연한 배우를 Folded Graph로 표현할 수 있다.

Representing Graphs : Adjancency Matrix

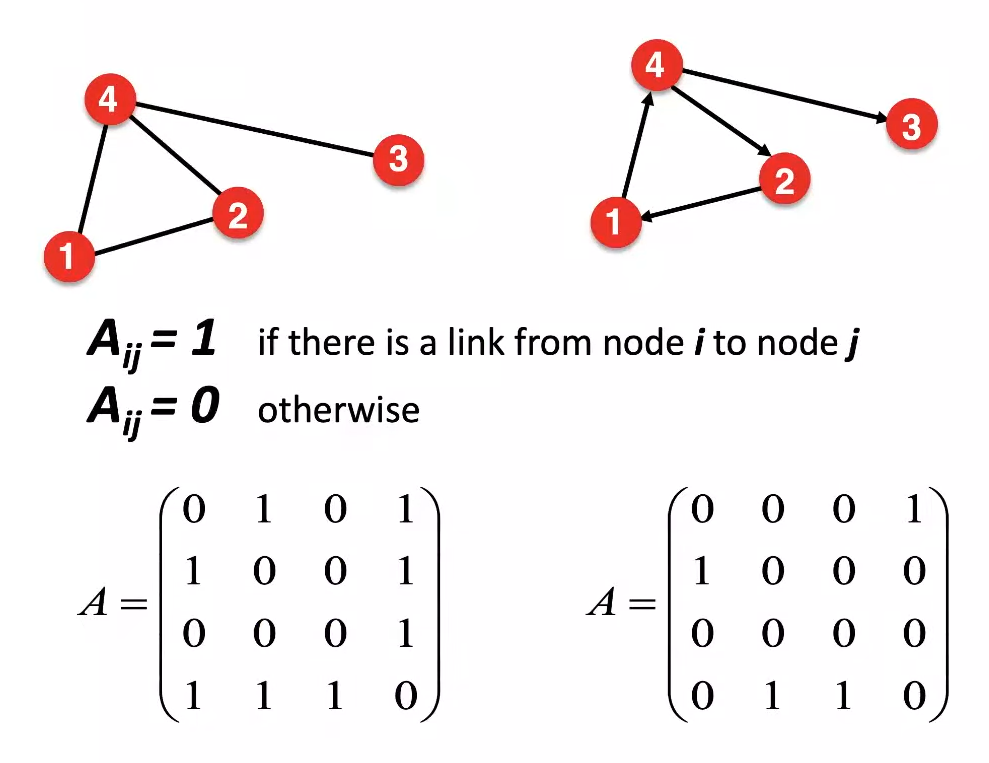
Adjacency Matrix는 Graph를 Matrix로 표현하는 방식이다. 각 node를 행과 열의 index로 하여, 연결된 경우 1, 연결되지 않은 경우 0으로 값을 정한다. 이때 Undirected Graph의 경우에는 Matrix가 대칭을 이루고, Directed인 경우에는 비대칭이 될 수 있다.

Node Degree를 구하고 싶은 경우에는 행/열의 값을 합하면 되며, Multi Graph(중복 가능한 Graph)의 경우에는 0/1 외에도 더 큰 숫자를 넣을 수 있다. 또한 loop의 경우에는 행과 열의 index가 같은 곳에 1을 넣으면 된다.

단점은 실세계의 경우, 연결되지 않은 Node들이 압도적으로 많으므로 데이터의 낭비가 심할 수 있다.

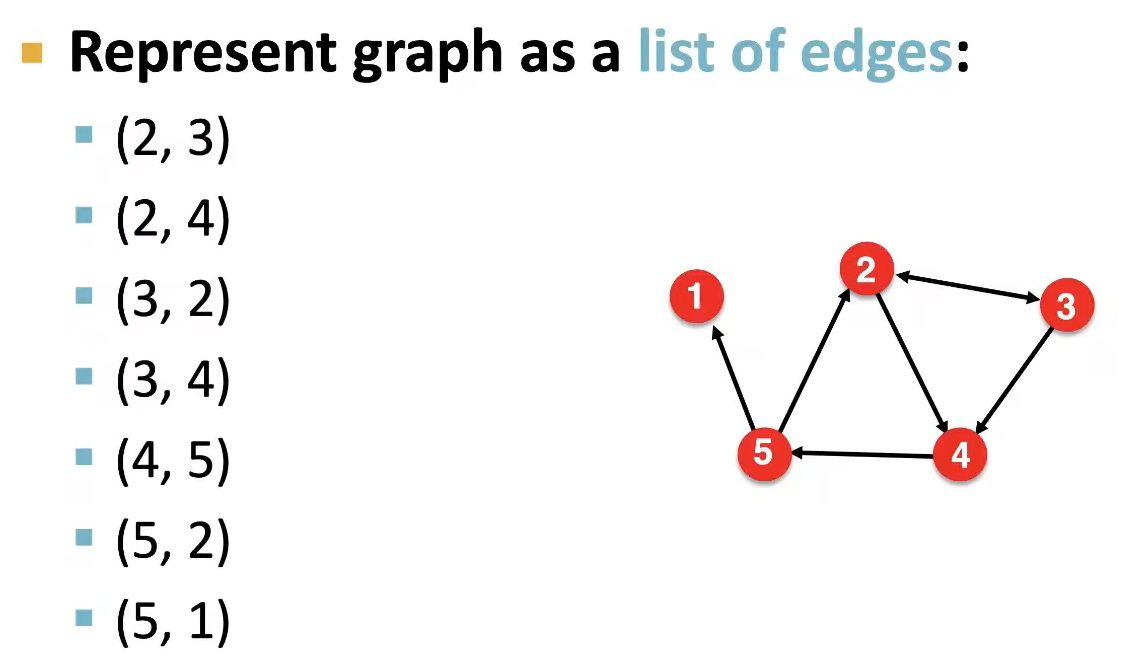
Representing Graphs : Edge List

Edge List는 Adjacency Matrix의 데이터 낭비문제를 극복한 형식이다. Edge List는 말 그대로 Edge들의 출발점과 도착점의 index를 나열하여 Graph를 표현한다. 따라서 크고 밀도가 낮은 네트워크에서 유용하게 사용할 수 있다.

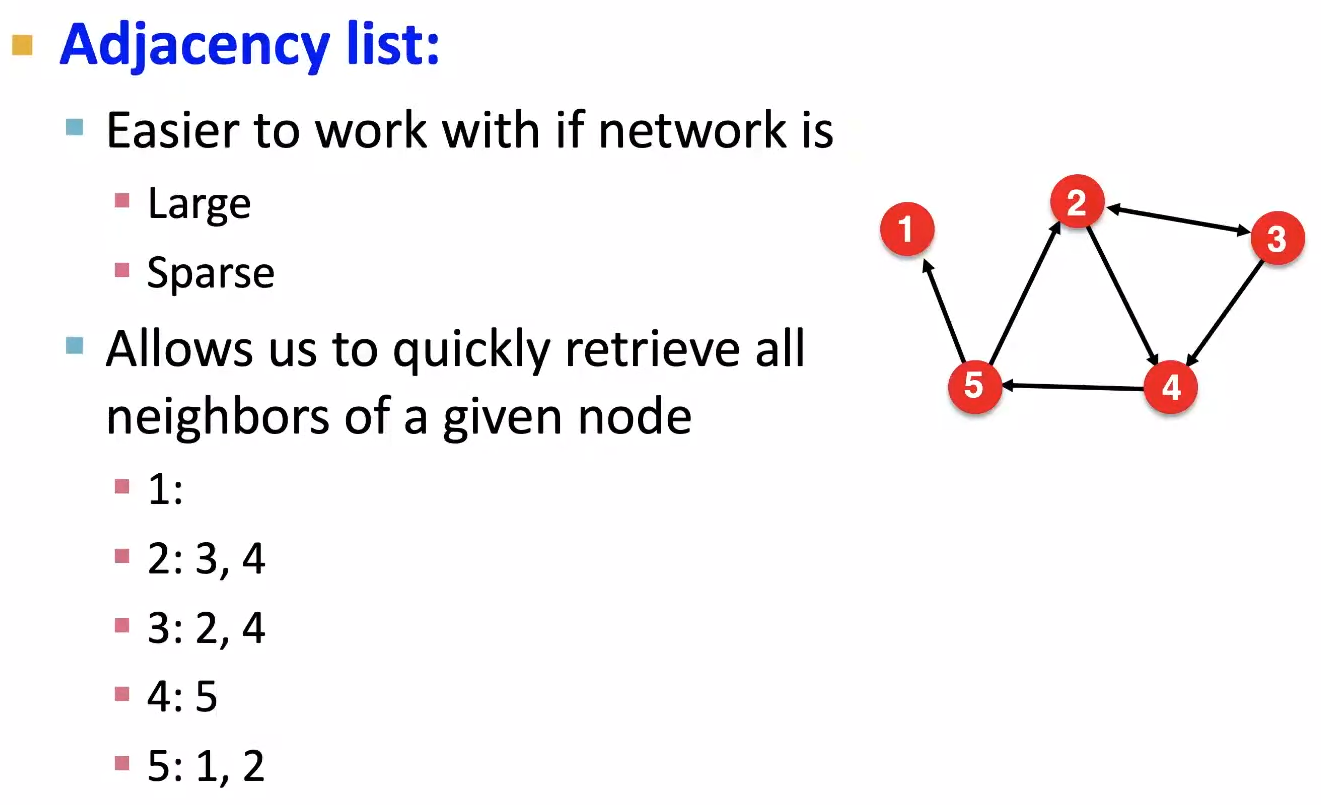
Representing Graphs : Adjacency List

Adjacency List는 Edge List와 유사하다. Adjacency List는 출발 Node를 기준으로 도착 Node(Undriected인 경우 인접 Node)들을 나열하여, Neighbor를 빠르게 찾을 수 있게 한다.

Node and Edge Attributes

이전에 설명했던 Graph들 처럼 Node와 Edge로만 이루어진 그래프 뿐만 아니라 여러 Attribute들을 가진 Graph 또한 존재한다.

1. Weight

Weight는 모든 Edge를 동등하게 취급하지 않고 차별화를 하기 위해 사용된다.

e.g., frequency of communication

2. Ranking

Ranking은 Edge에 순서(우선순위)를 부여하기 위해 사용된다.

e.g., best friend, second best friend…

3. Type

Type는 Edge에 관계의 종류를 부여하기 위해 사용된다.

e.g., friend, relative, co-worker

4. Sign

Sign은 Edge를 구분짓기 위해 사용된다.

e.g., Friend vs. Foe, Trust vs. Distrust

이 외에도 다양한 Attribute들이 존재할 수 있다.

1강 Summary

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 1.3 - Choice of Graph Representation​