Message Passing

Loopy Belief Propagation을 이해하기 위해 Message Passing의 기본적인 개념을 먼저 짚고 넘어가보자.

Message Passing의 기본 전제는 이전 Node로부터 메시지를 받으면 해당 메시지를 업데이트하고, 다음 Node로 넘기는 것이다. 이때, 기본적으로 각 Node는 자신의 이웃에게만 Message Passing을 할 수 있다.

아래는 Message Passing을 이용하는 간단한 예시이다. Graph 내의 Node 수를 세는 것이 목표이며, cycle은 없다고 가정한다. 먼저 Node에 숫자를 부여하여 낮은 수에서 높은 수의 방향으로 edge가 향한다고 가정한다. 그리고 각 Node는 자신이 받은 메시지에 1을 더해서 다음 Node에게 넘긴다.

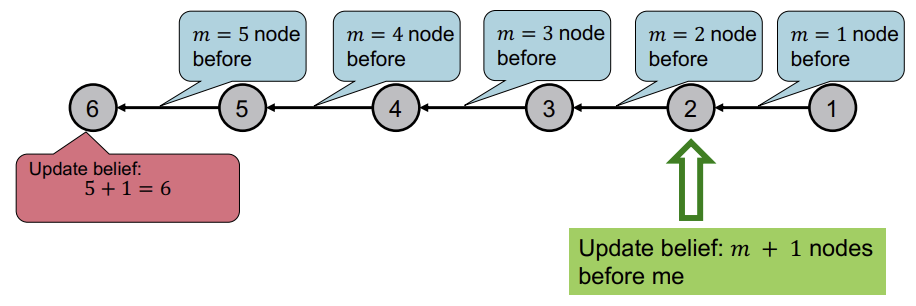
이러한 방식은 위와같은 선형 그래프 뿐만 아니라 leaf에서 root방향으로 Message Passing을 하는 형태로 구현하여 Tree에서도 사용 가능하다.

Loopy Belief Propagation Notation

먼저 Loopy BP Algorithm의 Notation부터 정리해보자.

- Label-label potential matrix \(\psi\)

\(\psi(Y_{i},Y_{j})\)는 Node \(j\)의 이웃 Node \(i\)의 Class가 \(Y_i\)일 때, \(j\)의 Class가 \(Y_j\)일 확률이다.

- Prior belief \(\phi\)

\(\phi(Y_i)\)는 Node \(i\)의 Class가 \(Y_i\)일 확률이다.

- \(m_{i \rightarrow j}(Y_j)\)

\(m_{i \rightarrow j}(Y_j)\)는 Node \(i\)가 Node \(j\)에게 보내는 메시지로, Node \(j\)의 Class가 \(Y_j\)일 확률에 대한 추정치를 담고있다.

- \(L\)

모든 Class 종류의 집합이다.

Loopy Belief Propagation Algorithm (No Cycle)

아래는 실제로 Loopy BP Algorithm이 동작하는 예시이다.

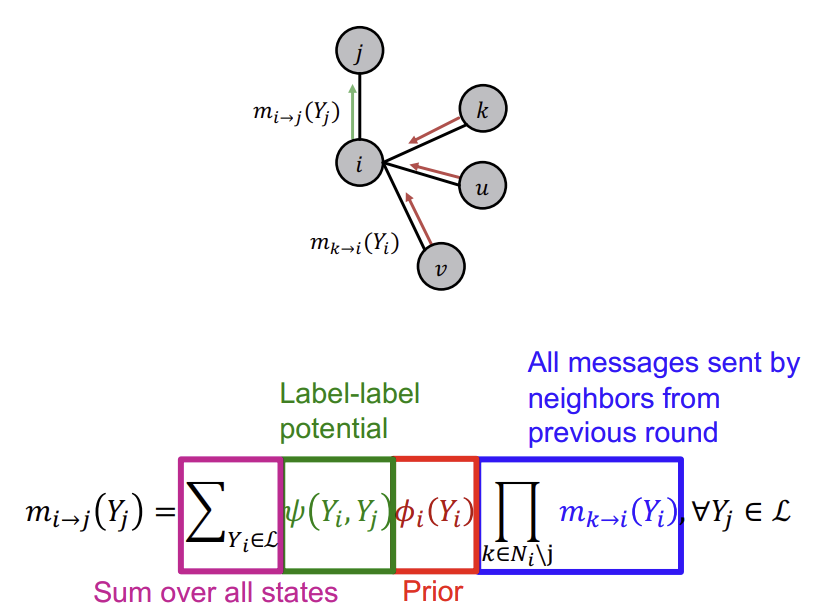
먼저 모든 메시지를 1로 초기화 한 후, Node \(j\)를 제외한 모든 이웃(하위 이웃)들로부터 Node \(i\)가 \(Y_i\)일 belief의 합(파란색)을 구한다.

이후, 그 값을 자신이 \(Y_i\)일 확률(빨간색)과 곱하고, 그 값을 다시 Node \(i\)가 \(Y_i\)인 경우 Node \(j\)가 \(Y_j\)일 확률(초록색)과 곱한다.

이 과정을 존재하는 모든 Class에 대해 진행하여 더하면, 그것이 바로 Node \(i\)가 Node \(j\)에게 보내는 메시지인 \(m_{i \rightarrow j}(Y_j)\)이다.

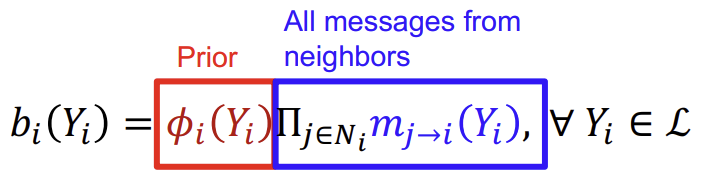
이렇게 converge된 값 \(b_{i}(Y_{i})\)가 Node \(i\)가 Class \(Y_i\)를 가질 확률에 대한 예측값인 것이다.

Loopy Belief Propagation Algorithm (With Cycle)

이제는 cycle이 존재하고, Node들의 순서가 없는 Graph에 대한 예시를 보자. 이러한 경우는 임의의 Node로부터 시작하여, 이웃 Node를 업데이트 하기위해 edge를 따라서 이동한다.

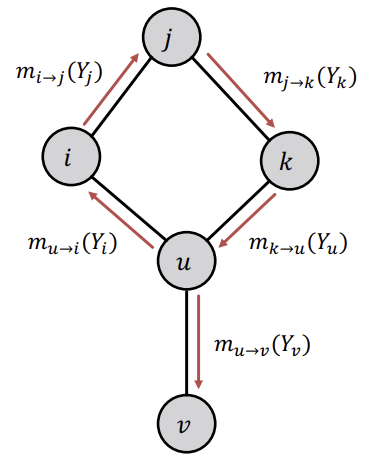
위와 같은 경우, 하위 Node로부터 전달받는 메시지가 더이상 independent 하지 않고, 상호 의존적이게 된다. 이로 인해 틀린 belief라도 cycle을 순환하면서 점점 reinforce되어 잘못된 결과를 도출할 수 있게 된다(random walk에서의 spider trap처럼).

아래의 예시 그림을 보면 T = 2, F = 1이라는 메시지가 Cycle을 돌며 T = 4, F = 1이라는 정보로 amplify 되는 것을 확인할 수 있다. 이런 방식으로 하나의 근거가 별개의 근거로 취급받고 점점 강화되는 것이다.

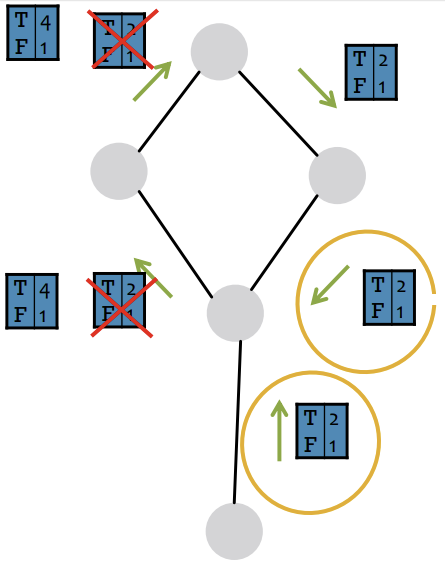
그럼 이런 문제를 어떻게 해결해야할까?

사실 실제로는 cycle의 영향이 이렇게 강하지 않다. 현실의 Graph들은 대체로 cycle이 매우 크고, cycle 내에 약한 edge를 하나라도 포함하기 때문이다.

이러한 Belief Propagation 방식은 프로그램을 짜기가 쉽고, 병렬연산 하기가 좋다. 또한 모든 Graph 모델에서 사용이 가능하며 semi-supervised node labeling을 할때 굉장히 강력한 algoritm/approach라는 장점이 있다.

하지만 loop가 많을수록 converge가 보장되지 않는다는 단점 또한 존재하며, Class 예측을 위한 Potential function은 학습과정을 거쳐야 한다.

Summary

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 5.3 - Collective Classification