Setup

GNN에 대한 설명을 시작하기에 앞서서,

graph \(G\)에 대해서

• \(V\)는 vertex의 set
• \(A\)는 adjacency matrix
• \(X \in \mathbb{R}^{m \times \vert V \vert} \)는 node feature의 matrix
• \(v\)는 \(V\)에 속한 node
• \(N(v)\)는 \(v\)의 neighbor의 집합

위와 같이 정의를 해두고 시작해보자.

A Naive Approach

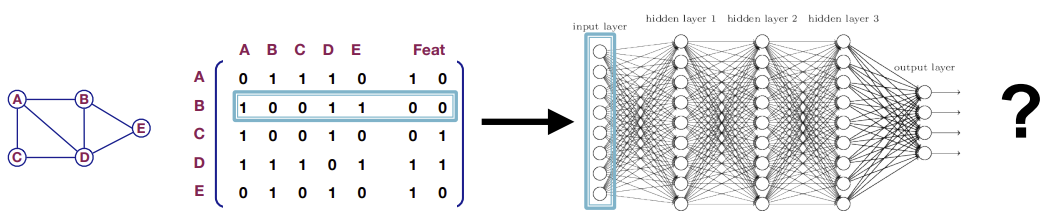
먼저 가장 간단하고 naive한 방식을 한번 생각해보자. 그냥 Graph의 Adjacency matrix에 Feature을 append해서 그걸 GNN의 input으로 사용하면 어떨까?

이 방식에는 여러가지 문제가 존재한다. 먼저 파라미터의 수가 node의 개수만큼 들어가게 되어 모델이 굉장히 무거워진다. 또한 training example이 1개밖에 없어 모델이 제대로 학습될 수 없고, graph의 크기가 달라지면 모델이 동작할 수 없게된다. 또한 원래 Graph에는 Node의 순서가 존재하지 않지만 Adjacency matrix는 순서에 의존적이기 때문에 모델이 Node의 순서에 sensitive하게 된다.

Idea : Convolutional Networks

Naive한 방법에서 위와같은 문제들이 발생하여 CNN 방식을 Graph에 generalize 해서 사용하고자 한다.

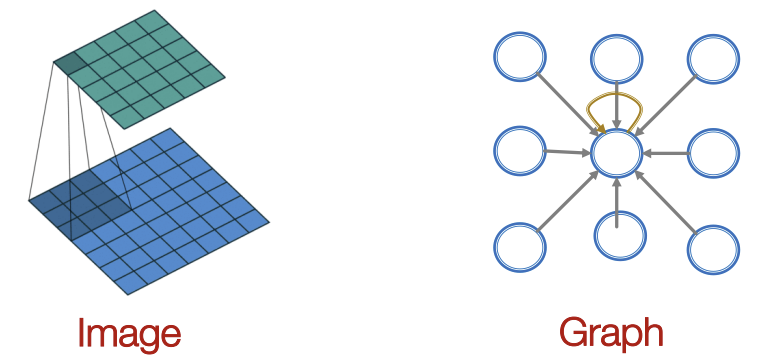
이미지에서 CNN을 사용할 땐 정해진 크기의 window를 이미지 전체에 특정 간격으로 slide하며 진행한다.

하지만 Graph는 이미지와 달리 격자형태가 아닌 복잡한 형태를 지니고 있어 window를 정의하고 sliding이라는 것을 정의하기 힘들다. 따라서 각 Node의 주변 이웃들로부터 메시지를 수집해서 하나의 새로운 메시지를 만드는 것이 아이디어이다.

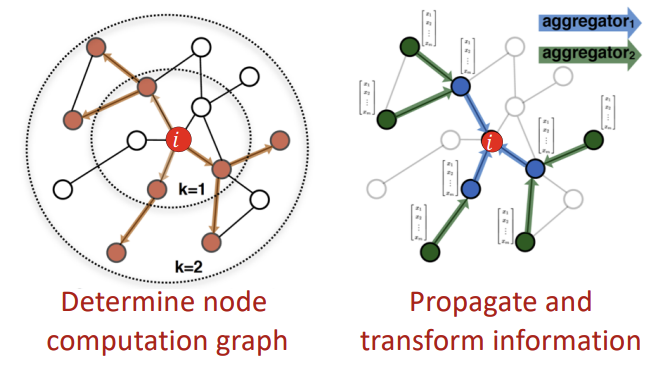
이를 위해 첫 step에서 Node Computation Graph를 정하고, 두번째 step에서 information을 transform/propagate한다. 이때의 Computation Graph가 Graph의 underlying하는 구조를 의미한다.

Idea : Aggregate Neighbors

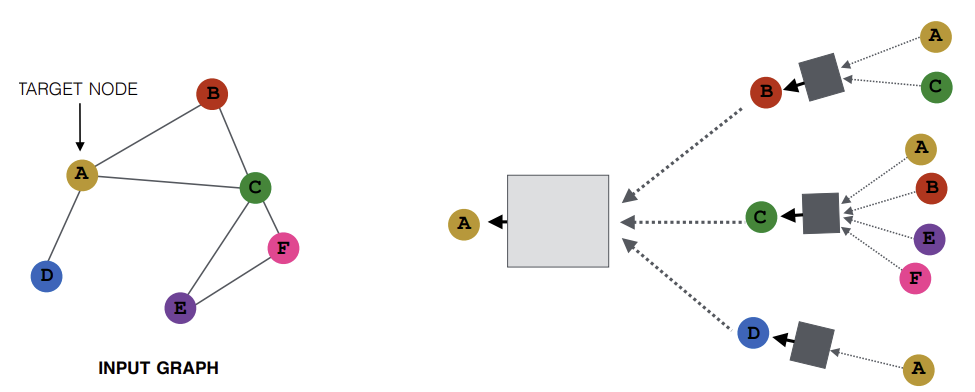
최종적으로 만들어진 형태가 위와 같이 이웃 간의 로컬한 네트워크 정보를 이용하여 Node Embedding을 만드는 방식이다. 이를 여러 layer로 만들면, 전체 네트워크에 대한 정보를 담을 수 있게 된다.

위와같은 Computation Graph를 모든 Node들이 갖는다. 이때 각 Node는 이웃들로부터 받는 정보들을 aggregate/transform 해서 본인의 정보로 만들게 된다.

가장 우측의 Layer인 0번째 Layer의 input으로는 해당 Node의 feature vector(ex. \(x_A\))가 들어간다. 그 다음 Layer부터는 이전 Layer에서 전달받은 정보와 자신의 feature vector의 정보를 합쳐서 다음 Layer로 전달한다. 따라서 모델의 깊이에 따라 예를들어 Layer-k embedding은 Target Node로부터 k hop 떨어진 Node들로부터 정보를 받는 것이다.

이때, 각 Node가 이웃들로 받은 정보를 aggregate/transform하는 과정에서 사용하는 함수는 순서에 무관해야하고, 함수의 파라미터가 학습이 되어야한다. 그러한 함수는 일단은 위 그림에서 네모 형태의 Black Box로 나타나 있다.

Neighborhood Aggregation

가장 기본적인 방식은 이웃의 정보를 평균내는 것이다. 이때 사용되는 공식은 아래와 같다.

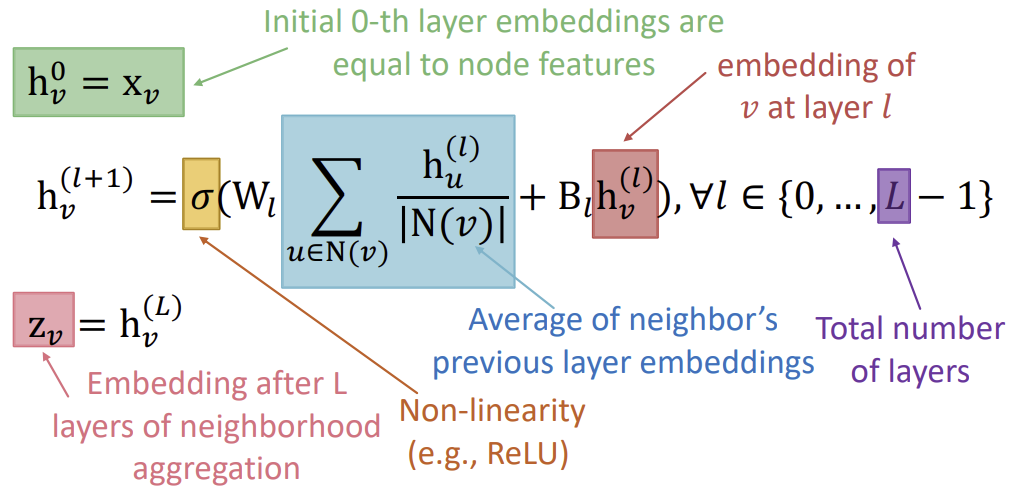
수식이 복잡해보이지만 내용은 단순하다.

윗 줄의 초록색 부분은 최초의 0번째 Layer의 Embedding이 Node feature와 같다는 것을 의미한다.

그 이후의 Layer를 계산할 때는 그 이전 Layer의 Embedding에 Matrix \(B_l\)을 곱하고, \(N(v)\)에 속하는 \(v\)의 이웃 \(u\)에 대한 Layer \(l\)의 Embedding의 평균을 구하여 matrix \(W_l\)을 곱한다.

그리고 그 둘을 더한 후, ReLU와 같은 non-linear 활성화 함수에 곱한다. 이를 \(l\)회만큼 여러 회차 iteration을 진행하면, 최종 Layer \(L\)에서의 Embedding(\(h_{v}^{(L)}\))은 결론적으로 \(z_v\)와 같게 된다.

이것이 Deep Encoder이다.

그렇다면 이러한 모델을 어떻게 학습시켜야 할까?

위에서 본 수식에서 우리는 weight Matrix \(W_l\)과 \(B_l\)을 학습시킬 수 있다. 이러한 Embedding을 loss function에 feeding하여 SGD를 통해 weight parameter를 학습시키는 것이다.

이를 위해 먼저 앞에서 본 수식을 행렬식으로 변경해보자.

Model Parameters

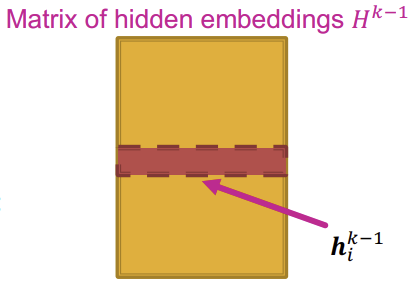
먼저 위와같이 모든 Node의 \(h^{(l)}\)값을 concat한 후, transpose하여 행렬 \(H^{l}\)로 만든다.

그리고 \(D\)를 diagonal matrix(대각선으로만 값이 있고 나머지는 0으로 채워진 행렬)로 정하고, 값은 \(D_{v,v} = Deg(v) = \vert N(v) \vert\)로 정하여 대각선마다 해당 행의 Node의 이웃 수가 되도록 한다. 그러면 \(D_{v,v}^{-1} = 1 / \vert N(v) \vert \)이 되므로 아래와 같이 공식을 치환할 수 있다.

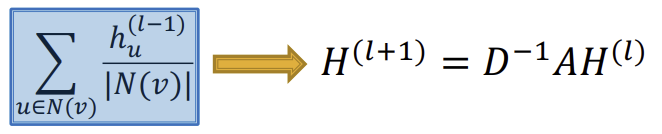
그리고 최종적으로는 아래와 같이 변형할 수 있다.

이러한 과정이 모든 GNN에서 가능한 것은 아니다. aggregation function이 복잡한 경우에는 행렬로 표현이 불가능 할 수 있다.

How to train a GNN

GNN을 학습시키는 과정은 이전 강의들에서 다룬 기본 NN 학습 과정과 유사하다.

Graph 내에서 유사한 Node들은 유사한 Embedding을 가질 것이므로, Graph 내에서의 유사도(\(y_{u,v}\))와 임베딩 공간에서의 유사도(\(z_u,z_v\))의 오차가 최대한 적도록 해야한다. 이때, Graph 내의 유사도는 random walk 등으로 측정할 수 있다.

이를 수식으로 나타내면 아래와 같고, \(y_{u,v}\)가 1에 가까울수록 \(u\)와 \(v\)가 유사하다. 그리고 CE는 cross entropy, DEC는 decoder를 의미한다.

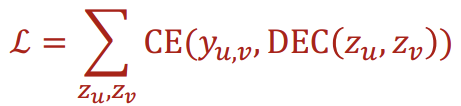
Cross entropy loss를 계산할 때는 아래와 같은 수식을 이용한다. 아래는 node classification task를 위한 수식이다.

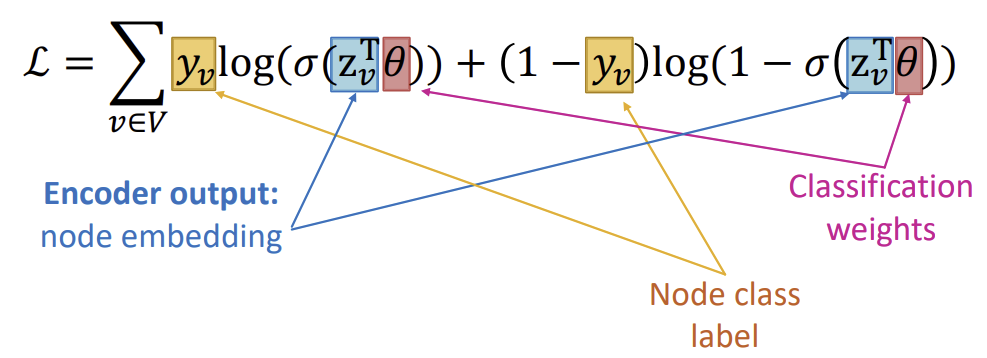
\(\sigma (z_{v}^{T} \theta)\)가 0에 가까우면 수식의 뒷부분이 남고, 1에 가까우면 수식의 앞부분이 남게된다. 예를들어 class label \(y_v\)가 0인 경우가 toxic, 1인 경우가 non-toxic이었다면, \(\sigma (z_{v}^{T} \theta)\)가 0에 가까운 경우 non-toxic, 1에 가까운 경우 toxic으로 classification 된다.

Model Design : Overview

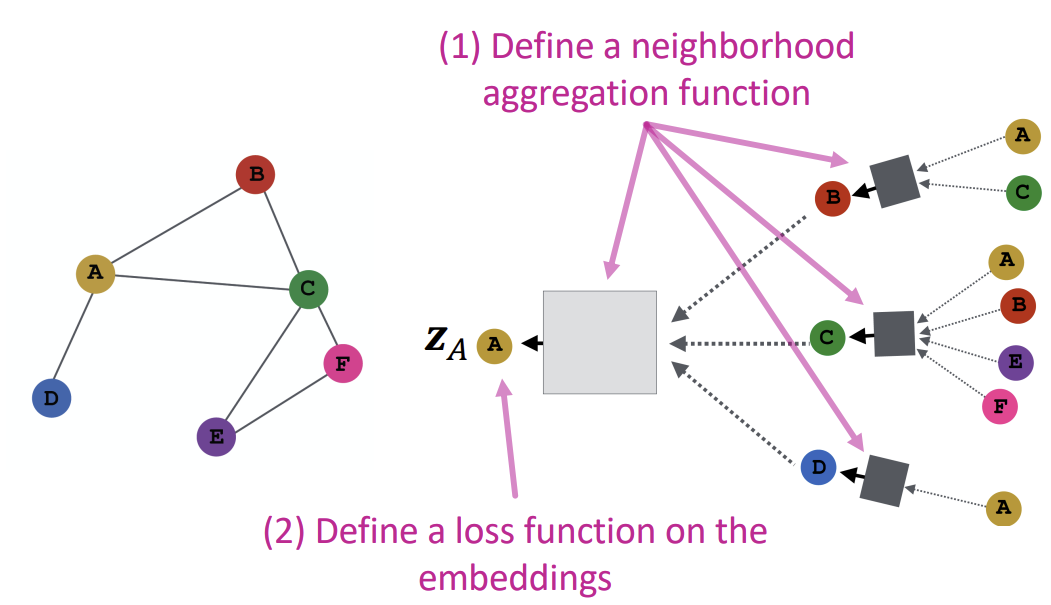
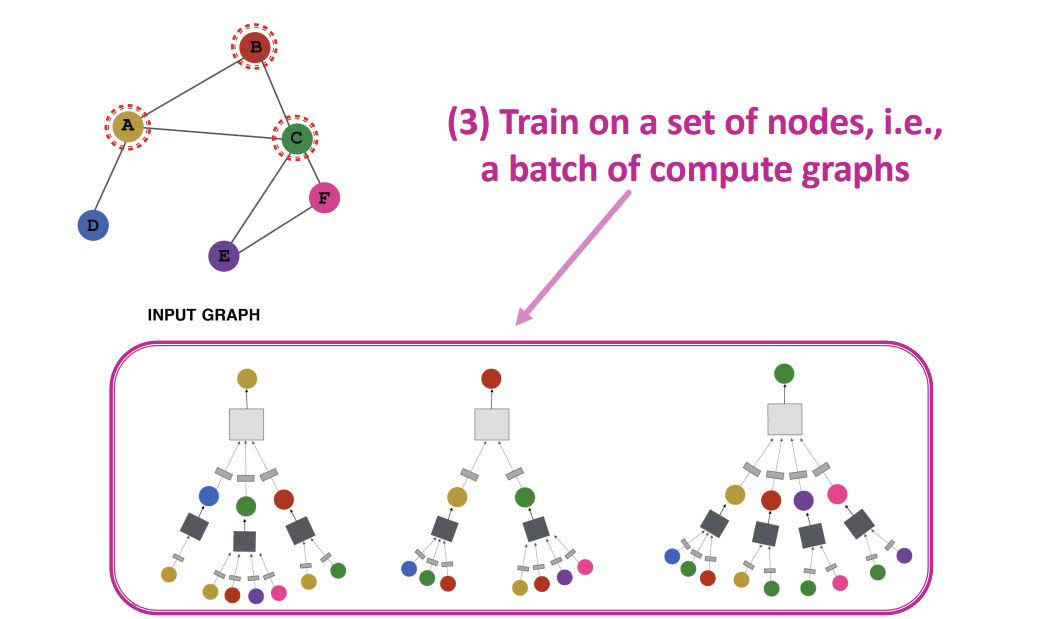
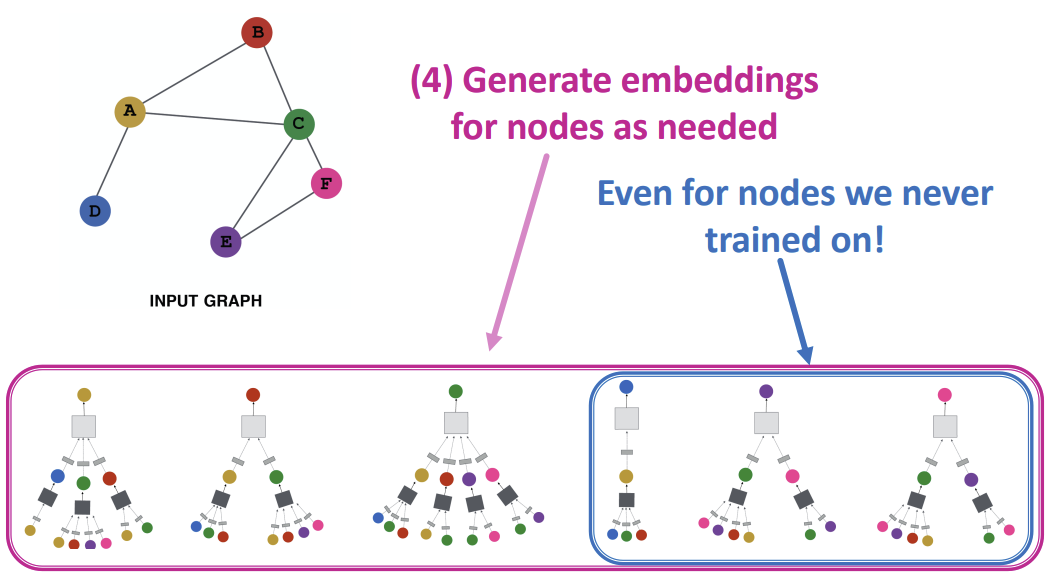
Inductive Capability

모든 Node들에 대해 parameter \(W\)와 \(B\)는 공유되어 사용된다. 또한 \(W\)와 \(B\)는 임베딩 차원과 크기에만 좌우되고, 그래프의 크기와 무관하게 사용할 수 있기 때문에, 한 그래프에서 학습시킨 모델을 다른 그래프에 적용시킬 수 있고, 시간에 따라 변화하는 그래프에서도 사용할 수 있다.

Summary

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 6.3 - Deep Learning for Graphs