Why Augment Graphs?
지금까지 배운 내용에 따르면 raw input graph = computational graph이다. 하지만 이러한 가정을 깨는 이유는 항상 완벽한 graph만 존재하는 것이 아니기 때문이다.
feature가 부족한 그래프는 feature augmentation으로, 그래프가 너무 sparse/dense/large한 경우에는 structure augmentation을 통해 학습을 용이하게 만드는 것이 Graph Augmentation의 목표이다.
Feature Augmentation on Graphs
Input graph does not have node features
Input으로 Adjacency matrix만 주어지는 경우, Node에 대한 feature가 전혀 주어지지 않는다. 이에 대한 해결책은 2가지가 존재한다.
첫번째는 각 Node에 동일한 constant value를 부여하는 방식이고, 두번째는 one-hot 방식으로 unique한 ID를 임의로 부여하는 방식이다.
이러한 두 방식에는 아래와 같은 장단점이 존재한다.
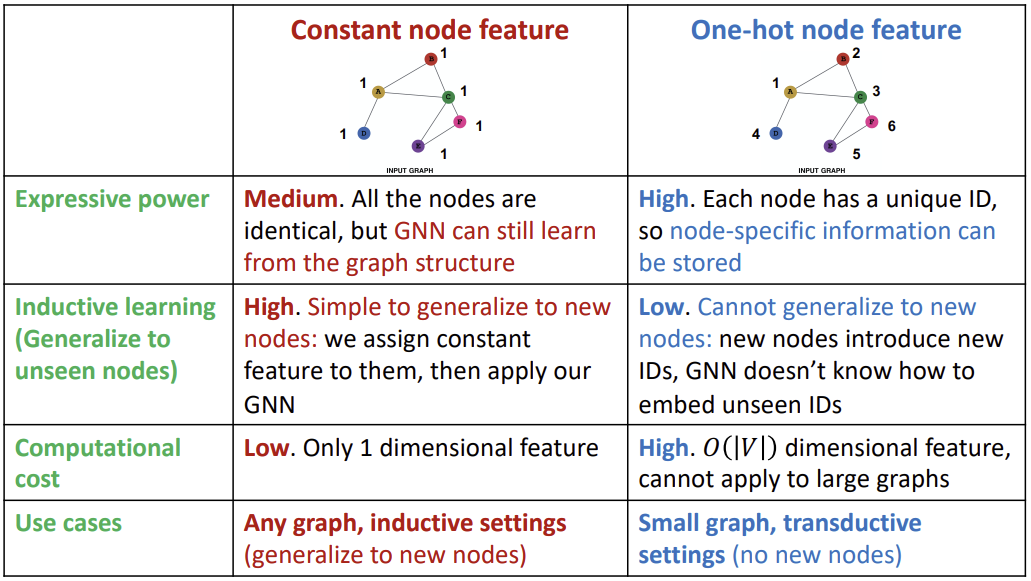
Certain structures are hard to learn by GNN
GNN으로 학습하기 어려운 구조들이 존재한다. 예를들면 어떤 Node를 포함하는 cycle의 크기를 계산하는 것은 해당 Node에 대한 computational graph의 형태가 동일하기 때문에 Node를 구분할 수 있는 feature가 없으면 상당히 어렵다.
이러한 문제를 해결하기 위해 cycle count를 나타내는 node feature를 추가하는 방식을 사용할 수 있다. 예를들어 아래 그림에서는 vector를 이용해 해당 Node가 크기가 얼마인 cycle에 포함되는지를 나태내고 있다.
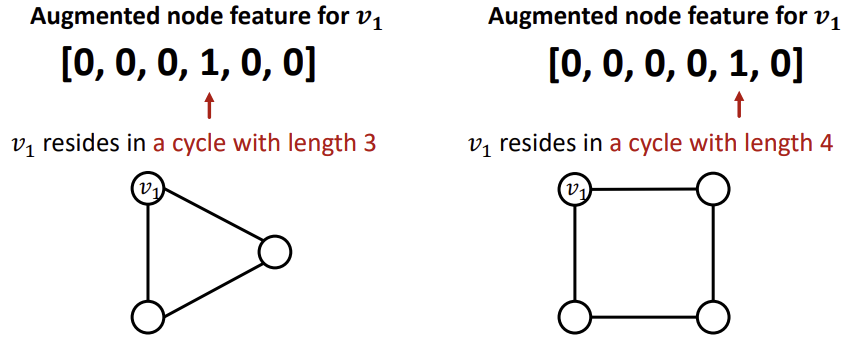
이 외에도 Node degree, Clustering coefficient, PageRank, Centrality 등 이전 강의들에서 배운 다양한 구조적 feature들을 추가할 수 있다.
Structure Augmentation on Graphs
Add Virtual Edges
Sparse한 그래프에서 message passing이 효율적으로 일어나지 않는 문제를 해결하기 위해 2-hop neighbor들 사이에 Virtual Edge를 추가할 수 있다. 이를 수학적으로 표현한다면, Adjacency Matrix를 사용할 때, 기본적인 Adjacency Matrix \(A\)를 사용하는 것이 아닌, \(A + A^2\)를 사용하면 \(A^2\)가 2-hop neighbor를 표현하는 Matrix이므로, 2-hop neighbor에 대한 virtual edge를 추가하는 것이라고 볼 수 있다.
이러한 방식은 Bipartite graph에서 같은 논문을 작성한 author들을 연결할 때 사용할 수 있다.
Add Virtual Nodes
마찬가지로 sparse한 그래프에서 virtual node를 추가하고, 그래프 내의 모든 Node들과 연결하는 방식을 통해 모든 Node들의 최단거리가 2는 되도록 만들 수 있다. 이를 통해 message passing을 굉장히 효과적으로 할 수 있다.
Node Neighborhood Sampling
그래프가 너무 커서 computational graph를 GPU가 감당할 수 없는 경우에는 Node Neighborhood Sampling 방식을 사용할 수 있다.
예를들어 팔로워가 아주 많은 인플루언서의 SNS 계정의 neighbor를 모두 계산하려면 computational cost가 너무 많이 든다. 이를 해결하기 위해 neighbor 중에 일부를 sampling하여 message passing에 사용하고 나머지는 버리면 computational cost가 가벼워지게 된다.
하지만 만약 무시한 Node가 아주 중요한 정보를 가지고 있었다면 학습에 지장이 갈 수 있으므로, 이러한 sampling을 여러회차에 걸쳐 매번 다르게 진행하면 모델을 robust하게 만들 수 있다.
출처, 더 궁금하다면?
Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 8.1 - Graph Augmentation for GNNs