Recap

- Node Embeddings

우리는 이전에 Node Embedding 방법에 대해서 배웠다.

Node Embedding은 Node를 d-차원의 임베딩으로 매핑하여, Graph에서 유사한 Node들이 임베딩 공간에서도 가깝게 하는 것이다.

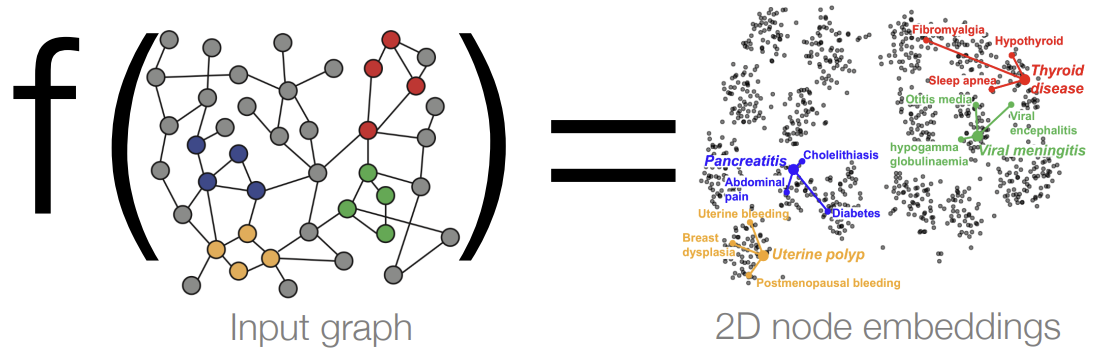
그렇다면 이때, 함수 f는 어떻게 학습해야 할까?

- Two Key Components

우리는 이를 위해 Encoder와 Decoder에 대해 정의했다.

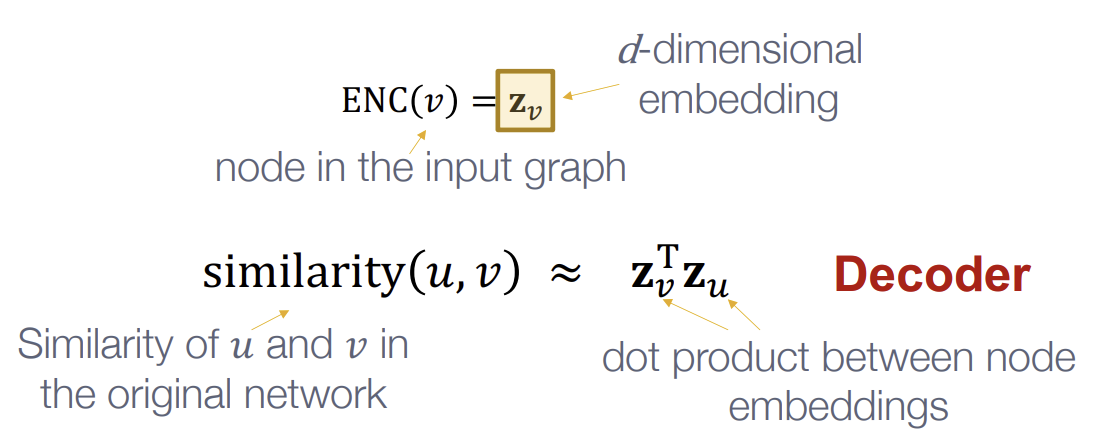
Encoder는 각 Node를 Low-dimensional vector로 매핑하고, Decoder는 vector 공간에서의 유사도와 원본 Network에서의 유사도가 얼마나 비슷한지를 구한다.

아래 그림에서 위 식이 Encoder, 아래 식이 Decoder의 역할을 보여준다.

- “Shallow” Encoding

우리가 이전에 배웠던 방식은 Shallow Encoding이다.

Embedding matrix가 존재할 때, Encoder는 Embedding을 look-up하는 역할만을 하는 것이다.

하지만 이러한 Shallow Encoder의 경우, \(O(\vert V \vert)\)개의 파라미터를 요구하고, inductive가 아니고 transductive하여, training 과정에서 학습하지 못한 embedding은 생성하지 못한다. 또한 Node feature를 활용하지 않는다는 단점들이 존재한다.

Deep Graph Encoders

6강에서 다룰 방식은 Graph Neural Network(GNN)이다. 해당 방식에서의 Encoder는 Graph의 구조를 바탕으로 여러 layer의 non-linear transformation을 수행한다. 이때, Random walk와 같이 이전에 배운 similarity function들을 결합하여 사용할 수도 있다.

아래 그림은 GNN의 구조를 나타낸다.

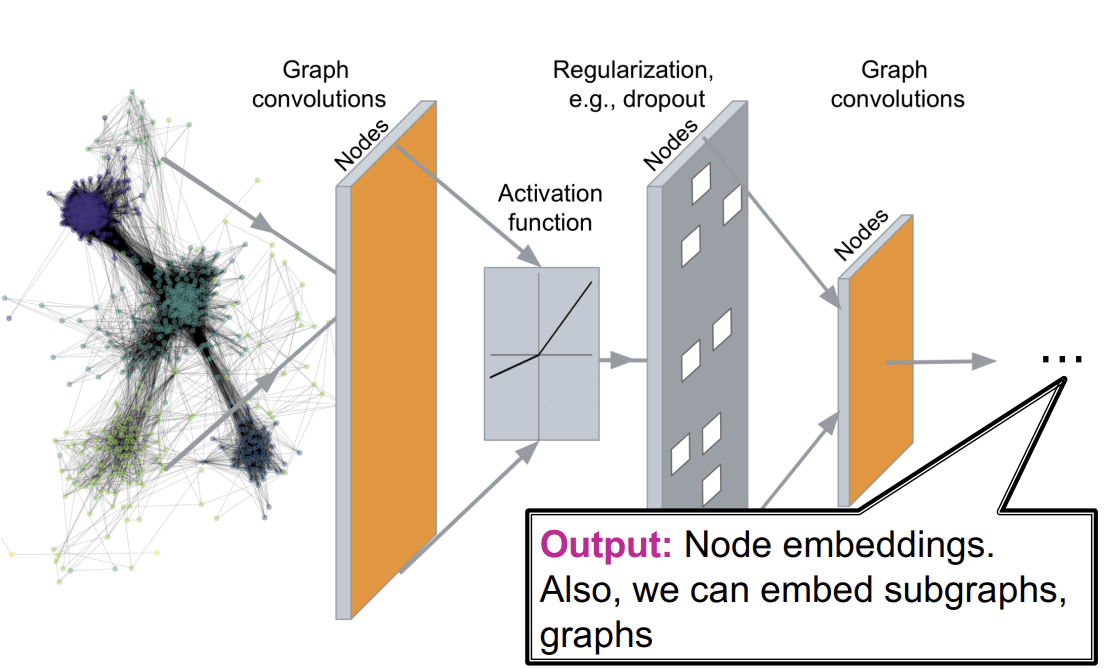
이러한 GNN 방식으로 Node Classification, Link prediction, Community detection(Clustering), Network similarity(유사한 subnetwork 찾기) 등의 Task를 수행할 수 있다.

GNN은 Traditional ML 방식과 달리, size가 정해져있지 않고, grid처럼 공간적인 locality가 존재하지 않아 topological한 구조가 복잡하다. 또한 node의 순서나, reference point도 존재하지 않고, multimodal feature들을 가질 수 있어 더 어렵다.

출처, 더 궁금하다면?

Stanford CS224W: ML with Graphs | 2021 | Lecture 6.1 - Introduction to Graph Neural Networks