Matrix Factorization

위 그림은 이전 강의에서 배웠던 Node embedding에 대한 설명이다. 유사한 두 노드 \((u, v)\)에 대해 \(z_{v}^{T}z_u\)를 최대화 하는 것이 이러한 Node embedding의 목표이다.

오늘 설명할 Matrix Factorization은 이보다 더 심플하다. 두 Node가 edge로 연결되어 있다면 이들을 유사하다고 정의하고, \(z_{v}^{T}z_u\)를 유사한 경우 1, 유사하지 않은 경우 0으로 만드는 것이다. 이는 다른말로 하면, \(z_{v}^{T}z_u\)를 adjacency matrix \(A\)에서의 \(A_{u,v}\)와 같게 하는, 즉, matrix 전체의 단위로 보면 \(Z^{T}Z = A\)로 만들고자 하는 것이다.

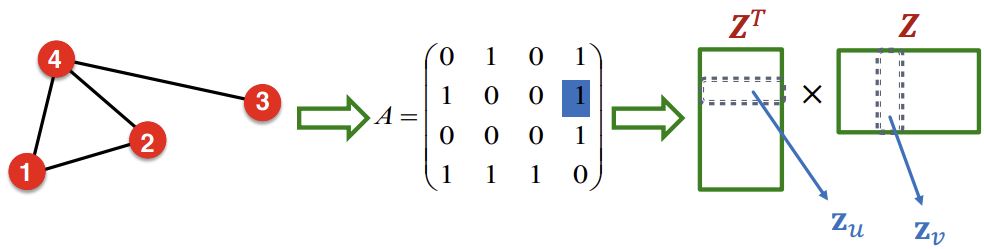
하지만 임베딩 matrix의 차원 d(d는 Z의 행의 갯수(=feature의 수)와 같다.)는 Graph 내의 Node의 수 n보다 많이 적다. 따라서 정확하게 \(A = Z^{T}Z\)가 되는것은 불가능하지만, 대략적으로 유사하게 하는것은 가능하다. 이를 위해 \(Z\)를 조정하여 \(A - Z^{T}Z\)가 0에 가깝게, 즉, L2 norm(Frobenius norm)이 최소가 되도록 하는것이 목표이다.

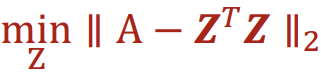
결론적으로, edge의 연결로 유사도를 정의한 내적 decoder는 adjacency matrix \(A\)의 matrix factorization과 같다.

Random Walk-based Similarity

Deepwalk나 node2vec은 더 복잡한 node 유사도의 정의를 가지고 있지만, 이 또한 matrix factorization으로 설명할 수 있다. 아래의 공식을 살펴보자.

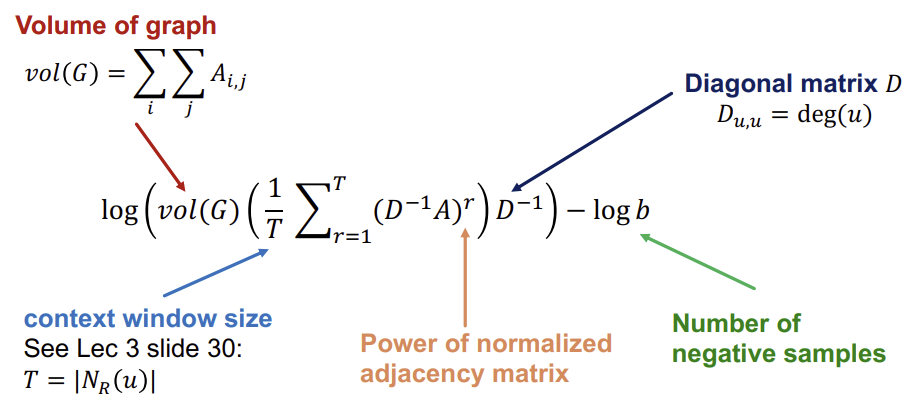
위 식을 기존 공식에서의 adjacency matrix \(A\)와 대체하여 \(- Z^{T}Z\)를 최소화하는 \(Z\)를 구하면 Random Walk based 임베딩을 구할 수 있다.

Node2vec 또한 matrix factorization으로 공식화 될 수 있다. 이는 Random walk보다 더 복잡하므로 해당 논문을 참고하자.

Limitation

이번 게시물에서 배운 Matrix factorization이나 random walk로 node embedding을 하는 방식에는 몇가지 한계점들이 존재한다.

첫째로, 노드가 시간에 따라 생겨나는 Graph(Social Network 등)의 경우에서, Embedding Matrix를 만들 당시에 없었던 Node는 임베딩을 갖지 못한다. 또한 새로운 Node에 대해 임베딩을 만들기 위해서는 Graph 전체의 Node Embedding을 계산해야한다는 불편한 점이 있다.

둘째로, 이러한 임베딩은 구조적 유사함을 포착할 수 없다. 아래의 예시를 보면 Node 1과 11의 local Network structure는 유사하지만, 완전히 다른 임베딩을 가질 것이다.

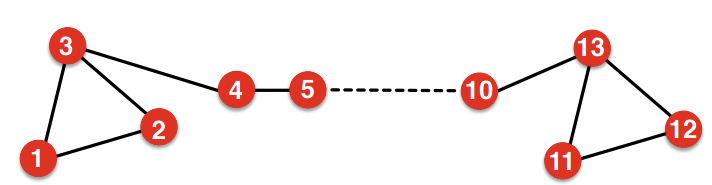
마지막으로 우리가 배운 임베딩으로는 Node, Edge, Graph 단위의 feature들을 구분하여 임베딩을 사용할 수 없다. 예를들어 단백질들 사이의 관계를 나타내는 Graph에서 특정 Node가 해당 단백질의 특성을 임베딩으로 가질 수는 없는 것이다.

이러한 한계를 극복하기 위해 Deep Representation Learning, Graph Neural Networks 등의 방식이 존재하는데, 다음 시간에는 Graph Neural Networks(GNN)에 대해 알아볼 것이다.

Summary

출처, 더 궁금하다면?

Stanford CS224W: ML with Graphs | 2021 | Lecture 4.4 - Matrix Factorization and Node Embeddings