Outline
오늘은 이후의 GNN으로 넘어가기 위한 개요이다.
우리가 앞으로 다룰 question은 특정 Node들에만 레이블이 존재하는 네트워크에서 나머지 Node들에도 레이블링을 하는 방법에 대한 것이다.
또한 이를 위해 어떤 노드가 믿을만하고, 어떤 노드는 신뢰할 수 없는지에 대해서도 판단해야할 것이다.
하지만 오늘은 그 이전에, semi-supervised node classification에 대해 배울 것이다.
Semi-Supervised Node Classification
semi-supervised node classification은 이름 그대로 몇개의 Node들에 대한 정보를 주고(semi-supervised), 나머지 unlabeled Node들을 레이블링 하는(node classification) 방식이다.
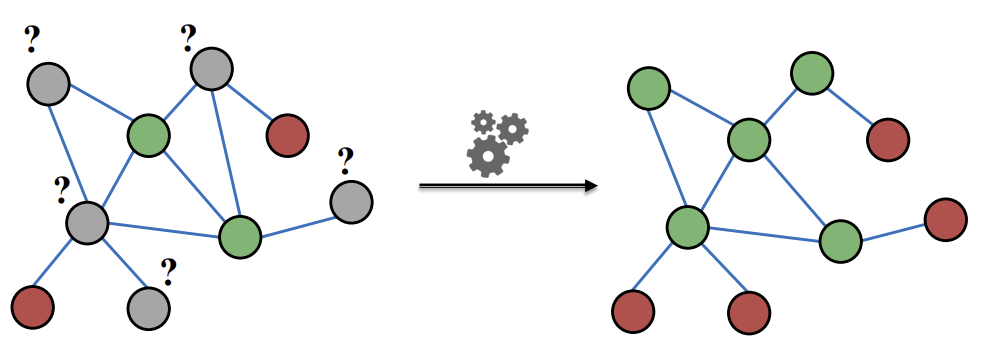
우리는 이를 message passing을 통해 하고자 한다. 이를 위해서는 네트워크 내에 Correlation이 존재한다고 가정하고, 이를 찾는 것이다. 이를 위해 아래 3가지 테크닉을 사용할 것이다.
- Relational classification
- Iterative classification
- Belief propagation
위 3가지 방식은 고전적이긴 하지만, 앞으로 이야기할 내용들에 대한 intuition을 준다.
Correlation
individual한 특징도 네트워크 내에서 연관되어 있다. Graph 내에서 이야기하자면, 가까운 Node들은 같은 색(= label, class)를 갖는 경향성이 있다.
correlation을 갖게하는 2가지 의존성이 존재한다.
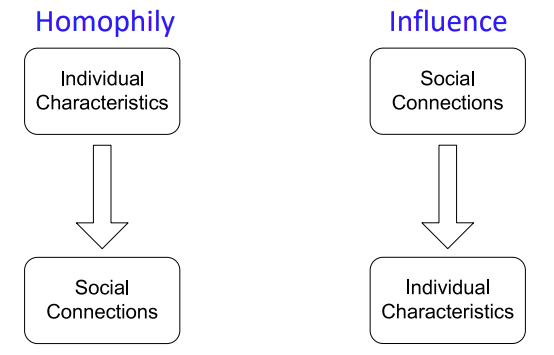
1. Homophily
Homophily를 한마디로 표현하면 “유유상종”이다. 즉, 유사한 관심사/취미를 갖거나 유사한 특성들을 가진 Node들끼리 관계를 맺게 되고, 가까워진다는 것이다.
2. Influence
Influence는 그와 반대로 “친하면 닮는다”이다. 이미 관계를 맺고 있는 Node들은 서로 영향을 주고받으며 유사한 관심사/취미를 갖게되거나 유사한 특성을 갖게 되는 것이다.
이러한 영향력을 주고받는 현상들을 어떻게 사용할 수 있을까? 한가지 방법은 “연좌제”이다.
label X와 연결되어있는 Node라면 label X를 가지고 있을 확률이 높다. 따라서 유해한 웹페이지와 같은 경우, 유해한 페이지와 link를 주고받는 페이지의 경우, 해당 페이지도 유해한 페이지일 것으로 추측할 수 있다.
Collective Classification 이 외에도 아래와 같은 다양한 분야에서 활용 가능하다.

Collective Classification Overview
correlation을 이용하여 연결된 Node들을 순차적으로 classification을 진행하고자 한다. 이를 위해 Markov Assumption을 사용할 것이다. 이는 Node\(v\)의 label\(Y_v\)가 Node\(v\)의 직속?(거리가 1인) 이웃들 \(N_v\)에 의해서만 결정되도록 하는 방식이다. 이를 식으로 나타내면 아래와 같다.
\[P(Y_{v}) = P(Y_{v} \vert N_{v})\]
Collective Classification은 다음 3가지 단계를 가진다.

1. Local Classifier
Local Classifier는 색이 없던 Gray Node들에게 initial한 레이블을 부여해준다. 이에 Node의 attribute와 feature정보를 이용한 기본적인 Classification 방식이 사용되고, 네트워크에 대한 정보는 사용되지 않는다.
2. Relational Classifier
Relational Classifier는 Node들 간의 correlation을 찾아서 classifier가 이웃의 label/attribute을 이용해 Node 레이블링을 하는 과정이다. 이 과정에서 네트워크에 대한 정보가 사용된다.
3. Collective Inference
Collective Inference 과정에서는 네트워크가 converge 되거나, 사전에 정해둔 수의 iteration이 채워질 때까지 네트워크 전체의 correlation을 반복적으로 전파하는 과정이다. 이 과정에서 네트워크 구조가 최종 결과에 영향을 미친다.
Problem Setting
앞으로 해결하고자 하는 문제는 다음과 같다.
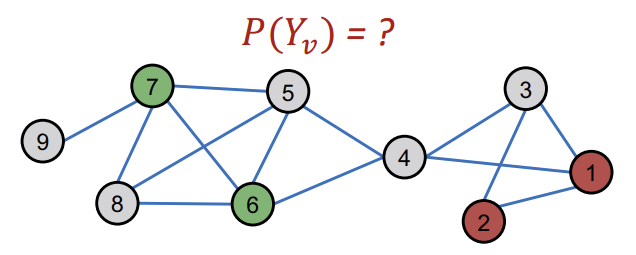
Unlabeled Node \(v\)의 label \(Y_v\)를 어떻게 예측하느냐?
각 Node \(v\)는 feature vector \(f_v\)를 갖는다.
몇몇 Node들은 \(\color{green}0\)또는 \(\color{red}1\)의 label을 가진다.
모든 feature와 Network가 주어졌을 때, \(P(Y_{v})\)를 구하라.
Overview

출처, 더 궁금하다면?
Stanford CS224W: ML with Graphs | 2021 | Lecture 5.1 - Message passing and Node Classification