2강 Recap

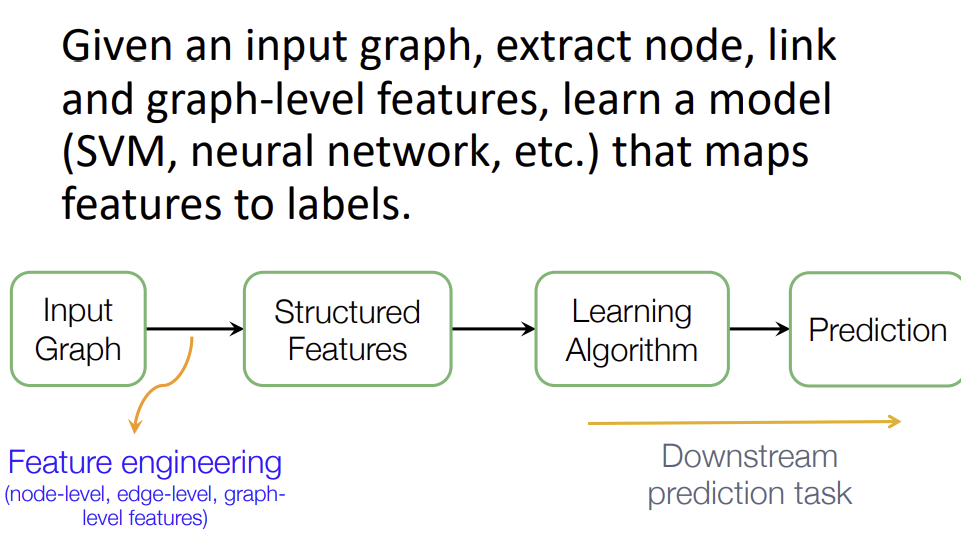
2강에서 배운 전통적인 Graph기반의 ML을 진행할 때, 대부분의 노력은 feature engineering에 들어간다. 이러한 feature engineering을 automatical하게 할 수 있을까? 이에 대한 해결책으로 3강에서는 representation learing에 대해 설명한다.

Graph Representation Learning의 목적은 Graph를 이용한 ML에서 유용한 feature learning이고, 이를 위해 embedding이라는 방식을 사용한다.

Why Embedding?

Embedding이란, Node를 d-dimentional space로 설명하는 방식으로, Node의 임베딩 유사성이 곧 Network 내에서의 유사성과 같게 만드는 것이 목표이다.

아래 그림에서 좌측은 Network, 우측은 해당 Network를 Embedding 하여 표현한 것이다.

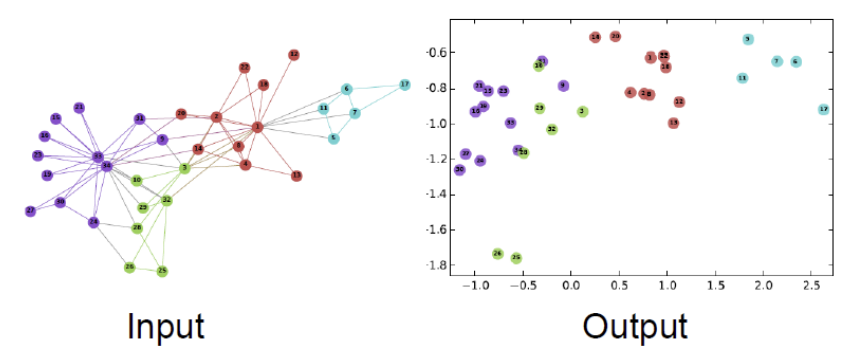
Node Embedding

이번 강의에서 우리는 undirected Graph를 adgacency matrix로 표현할 것이다. 그리고 그 외의 feature나 attribute에 대한 표현은 하지 않을 것이다.

위에서 말했듯 Node embedding의 목표는 embedding 공간에서의 유사성이 graph 공간에서의 유사성과 같게 하는 것이다. 그렇다면 이러한 유사성은 어떻게 판단할까? 이번 강의에서 embedding 공간에서의 유사성은 dot product로 정의한다. Dot product는 기준점에 대한 두 Node의 각도의 코사인값으로, 둘의 거리가 가깝거나 둘의 각도(방향)이 유사하면 커진다. 그리고 둘의 각도가 90도에 가까울수록 유사성이 0에 가까워진다.

그렇다면 이제 Graph 공간에서의 유사성을 정의하고, 이를 이용해 Learning을 진행해야 한다.

앞으로의 강의 내용을 요약하자면 아래와 같다.

Encoder

Encoder는 각 Node를 d-dimensional vector(일반적으로 d는 64 ~ 1000)로 embedding 하는 역할을 하고, Decoder는 Similarity function으로 구해진 network에서의 유사도와 vector space에서의 유사도를 비교하고 처리한다.

단순하게 생각하면 Encoder는 그저 embedding-lookup이다. 즉, 한 node를 input으로 받아, embedding 공간에 놓는 것이다.

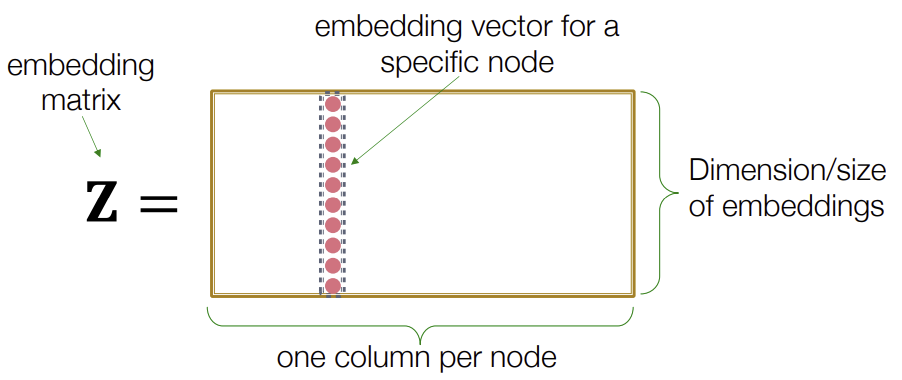
위 공식을 보면 embedding matrix Z에 v를 곱함으로써 해당 Node의 feature를 나타내는 한 column만을 추출해낸다.

Node Similarity

Embedding matrix 내에서의 유사도는 dot product로 한다는 것을 이제 완벽하게 이해했다. 그렇다면 Graph 내에서는 어떻게 Node 유사도를 정의할 것인가? 이전 강의들에서 여러가지 방법론을 배웠다. Link의 수, 공유 neighbor의 수 등. 하지만 이번에는 random walks를 통해 Node 유사도를 측정할 것이다. 이때, unsupervised한 방법을 사용하고, task independent(해당 Network에만 적용되는) 학습법을 사용한다.

이에 대해서는 다음 강의에서 계속하도록 하겠다.

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 3.1 - Node Embeddings