Introduction

이번 강의에서는 Graph를 Matrix로 보고 대하는 방법에 대해 이야기 할 것이다. 그리고 저번 강의에서 배운 Random walk를 이용해 Node의 중요도를 정의하는 방법, PageRank에 대해 배우고자 한다.

PageRank는 Google Algorithm이라고 불리기도 하는데, PageRank가 Google의 Search가 존재하도록 만든 알고리즘이기 때문이다.

인터넷 웹, 논문의 citation, 위키피디아의 reference 등을 directed graph로 나타낼 수 있지만, 모든 웹페이지의 중요성이 같지는 않다. 이러한 Node들의 중요도를 rank하기 위해 Graph의 link 구조를 분석해야한다.

강의를 진행하며 아래 3가지의 중요도 계산 방법을 배워볼 것이다.

• PageRank

• Personalized PageRank (PPR)

• Random Walk with Restarts

PageRank : The “Flow” Model

가장 단순하게 생각하면 link의 수를 중요도로 매길 수 있다(Links as Votes). 이때, out-link의 수는 해당 Node가 마음대로 늘릴 수 있으므로, in-link의 수를 세는 것이 더 합리적이라고 할 수 있다.

그렇다면 in-link를 중요도로 정하면 될까?

그것도 문제가 있다. 모든 in-link의 중요도가 동일하지 않고, 더 중요한 페이지로부터 오는 in-link가 더 중요하기 때문이다. 그럼 다시 해당 페이지의 중요도를 알아야하는 재귀적인 상황이 발생한다.

이를 수학적으로 표현하기 위해 다음과 같은 방법을 사용한다. \(i\)라는 Node의 중요도를 \(r_i\)라고 하고, \(i\)가 \(d_i\)개의 out-link를 가진다고 하자. 이때 각 out-link에게 \(r_{i}/r_{d}\)의 중요도를 부여하고 이를 in-link로 하는 Node에게 전달하는 것이다. 이것이 PageRank의 개념이다.

이를 그림과 수식으로 표현하면 아래와 같다.

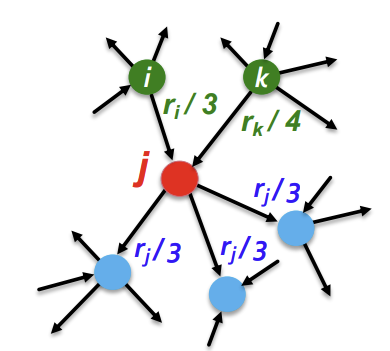
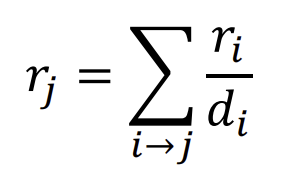
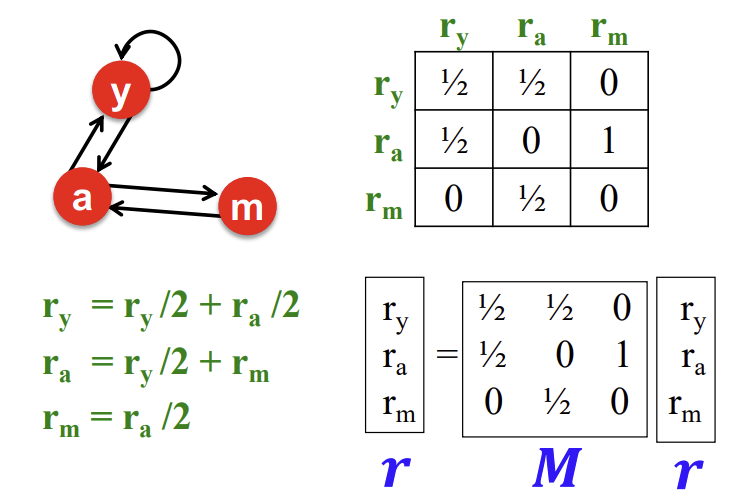
그렇다면 아래와 같은 Graph를 살펴보자.

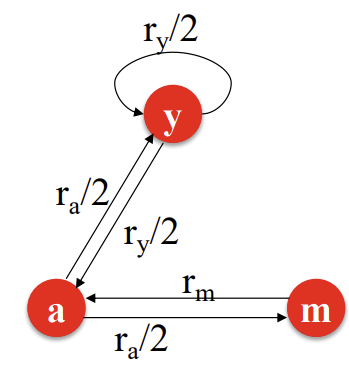
이런 경우, 아래 3개의 방정식이 성립한다.

\[r_{y} = r_{y}/2 + r_{a}/2\] \[r_{a} = r_{y}/2 + r_{m}\] \[r_{m} = r_{a}/2\]

그리고 여기에 중요도의 총합이 1이라는 정의를 추가하면?

\[r_{y} + r_{a} + r_{m} = 1\]

연립일차방정식을 가우스 소거법으로 풀 수 있(긴하)다. 하지만, 우리는 이보다 엘레강스 한 방법을 배워보자.

PageRank : Matrix Formulation

Graph를 이제 Stochastic adgacency matrix M을 정의해보자. 이 matrix는 column을 out-link가 향하는 Node로, row를 in-link가 들어오는 Node로 한다. 그러면 각 column의 합은 1이 되고, 이는 확률 분포를 의미한다.

추가로 Rank vector r을 정의하자. 이 vector의 각 index에는 해당 Node의 중요도 값이 들어가있고, 총합이 1이 된다. 그러면 아래와 같은 식이 성립한다.

\[r = M \cdot r\]

그리고 이는 위에서 사용한 아래의 식과 형태만 다르고 의미적으로 같다.

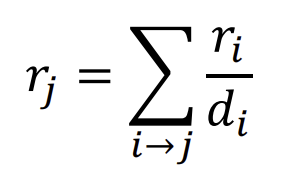
이러한 행렬 연산 과정을 예시로 보면 아래와 같다.

Connection to Random Walk

수식적으로 풀어보았으니 이제 직관적으로도 이해해보자. 이제는 PageRank를 이전에 배운 Random Walk와 연결지어 생각해보려고 한다.

uniformly(모든 확률이 동등하게) random하게 out-link를 클릭하며 웹서핑을 하는 사람이 있다고 가정해보자. 이러한 과정이 무한하게 지속되면 웹서퍼는 어디에 존재하게 될까?

서퍼가 \(t\)라는 시점에 \(i\)라는 페이지에 존재할 가능성을 \(p(t)\)라는 벡터에서 i번째에 들어가는 값이라고 하자. 그러면 \(p(t)\)는 페이지들에 대한 확률분포가 된다.

그러면 \(t+1\) 시점에 웹서퍼는 행렬 \(M\)에 \(p(t)\)를 곱한 확률 분포를 가지게 된다.

그렇다면 어느 시점에 웹서퍼가 \(p(t+1) = M \cdot p(t) = p(t)\)인 상태에 도달했다고 가정해보자. 이 지점에서는 stationary distribution(정적분포) 상태가 된다. 그리고 이는 이전에 살펴본 \(r = M \cdot r\)과 같으므로, \(r\) 자체가 random walk에서의 stationary distribution이라는 의미이다.

이러한 flow 기반의 수식이 flow로 해석될 수도 있고, 방금과 같이 무한히 random walk하는 사람이 시작지점과 무관하게 stationary distribution한 곳으로 회귀하는 것으로 해석할 수도 있다. 이를 계산하는 것이 곧 위에서 보았던 재귀적인 수식을 계산하는 것과 동일한 것이다.

여기서 한가지의 관점을 더 추가해보자.

위에서 본 \(r = M \cdot r\) 식을 \(1 \cdot r = M \cdot r\)이라고 본다면, 이는 eigenvector/eigenvalue 공식과도 구조가 같아진다. 즉, \(M\)이 1이라는 eigenvalue를 가질 때, eigenvector가 \(r\)인 것이다.

그리고 이때의 r은 \(M(M(M(…Mu)))\)처럼 웹서퍼가 \(u\)에서 시작하여 무한히 많은 random walk후의 위치이다.

다음 포스트에서는 이러한 \(r\)을 효율적으로 구하는 방법인 Power Iteration에 대해 배워보도록 하겠다.

summary

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 4.1 - PageRank