Power Iteration

이전 강의에 이어서 설명하자면, r을 구하기 위해 iterative한(반복적인) 절차를 거쳐 r을 업데이트 한다. 각 Node에 initial한 PageRank를 부여하고, converge 될 때까지 반복 한다. 이 때, converge는 이전 시간의 값과 비교했을 때 변화량이 \(\varepsilon\)보다 작으면 converge한 것으로 본다.

일반적으로 50step 정도에 converge가 되므로 굉장히 scalable하다.

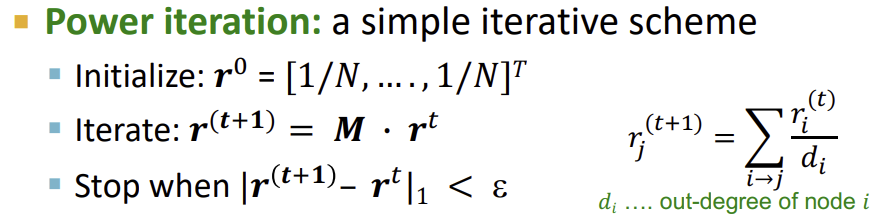
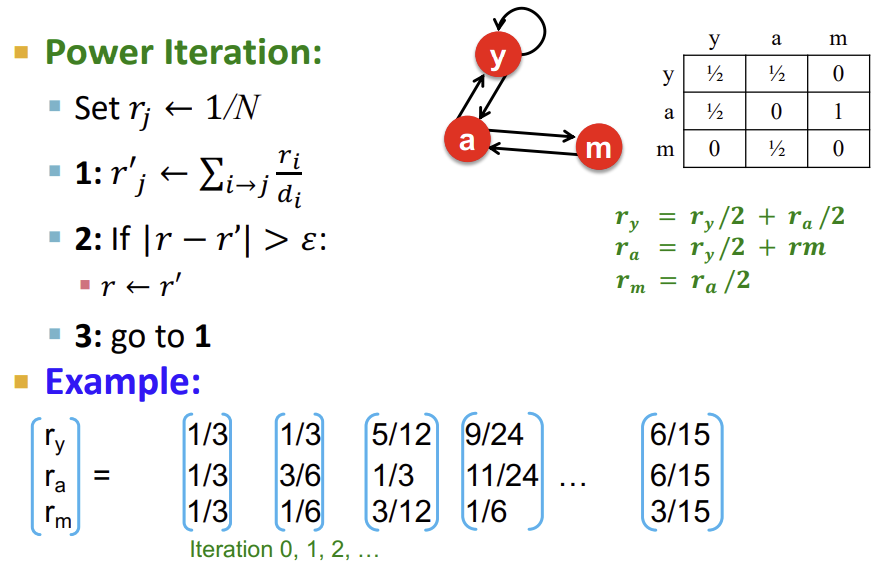
아래는 위의 내용에 대한 예시이다.

PageRank : Questions and Problems

이렇게 PageRank를 구하는 과정에서 우리는 3가지 궁금증이 생긴다.

• 과연 converge 하는가?

• 우리가 원하는대로 converge 하는가?

• 결과가 합리적인가?

그리고 위 3가지 조건에 모두 부합하는 PageRank를 설계하기 위해서 우리는 2가지의 문제를 해결해야한다.

• Dead Ends : out-link가 없는 Node
• 중요도가 새어나가 Graph 전체의 중요도를 0으로 만듦

• Spider Traps : out-link가 특정 Node 그룹 내에서만 돌도록 형성되어 있음
• 모든 중요도를 빨아들여 중요도를 독식함

다행히 위 2가지를 한번에 해결할 수 있는 방법이 존재한다. 바로 Random 순간이동이다.

Random Teleports

Spider trap을 방지하기 위해 Random walk 도중 확률적으로 Graph 내의 랜덤한 Node로 순간이동을 하고, out-link가 없는 Dead end를 만나는 경우엔 100% 확률로 순간이동을 하면(Graph의 모든 Node로 향하는 out-link가 있는 셈) 두 문제가 모두 해결된다.

아래는 random 순간이동까지 적용한 최종 수식이다. 참고로 일반적으로 순간이동이 발생하지 않을 확률인 \(\beta\)는 0.8~0.9로 설정한다.

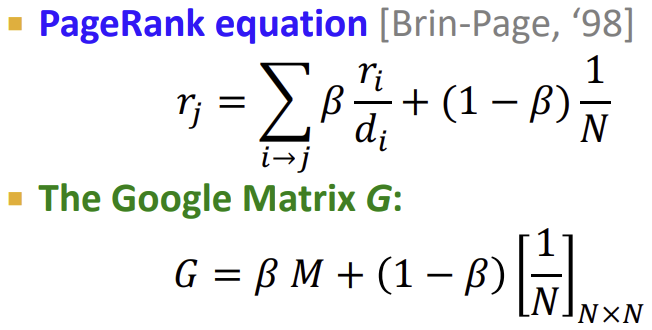
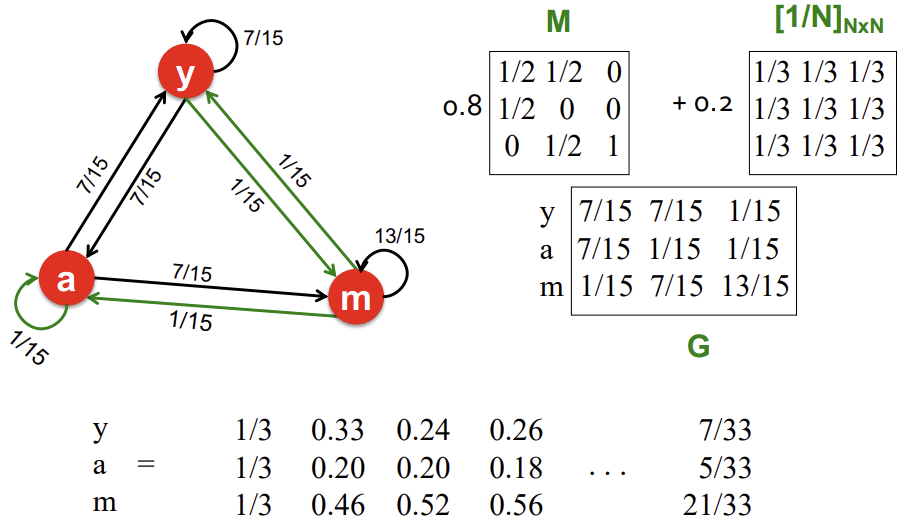
아래는 random 순간이동(초록색 화살표)를 추가한 예시 그림이다. 최종 converge된 결과를 통해 m > y > a의 중요도를 갖는다는 것을 확인할 수 있다.

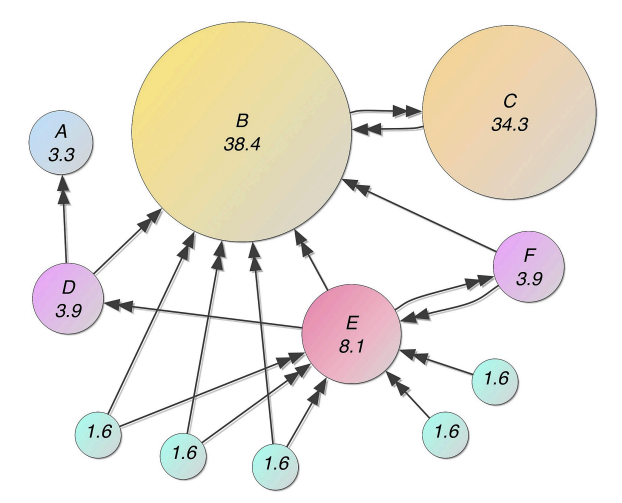
아래는 또다른 예시 그림이다. 위에서 언급했던 3가지 궁금증(필요)을 모두 해결한 모습이다. 또한 random 순간이동 덕에 중요도 점수가 0인 Node가 존재하지 않고, E와 in-link의 수는 같지만 중요한 Node로 부터의 in-link가 많은 B가 가장 중요한 모습을 보인다. 또한 C는 in-link가 하나뿐이지만 해당 link를 B로부터 받아 중요도가 높게 책정되는 모습이 우리가 원하던 합리적인 결과를 보인다.

Summary

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 4.2 - PageRank: How to Solve?