Notation

• Node u에 대한 embedding vector \(z_u\)

• u에서 시작한 random walk로 Node v에 도달할 확률 \(P(v \vert z_u)\)

• Softmax function : K개의 실수로 이루어진 vector를 총합이 1인 확률 K개로 변환시키기 위해 사용

\[\sigma_i(z) = \frac{e^{z_i}}{\sum_{j=1}^{K}e^{z_j}}\]

• Sigmoid function : 실수를 (0, 1)의 범위로 변환하기 위해 사용

\[S(x) = \frac{1}{1+e^{-x}}\]

Random Walk

출발 Node에서 연결된 edge를 따라서 랜덤하게 아무 neighbor Node로 정해진 횟수만큼 이동하는 것을 Random Walk라고 한다. 이때, 이미 지나온 edge를 중복해서 지나갈 수 있다.

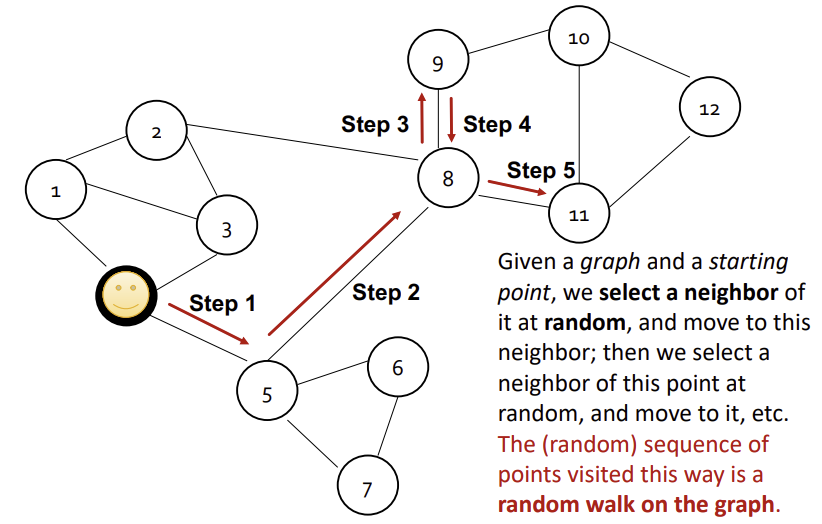
Node u와 v가 Graph 내에서 Random Walk를 통해 마주칠 확률이 Graph 내에서의 두 Node의 유사도이다.

이러한 Random Walk를 사용하는 이유는, 지엽적이거나 광범위한 범위에서의 유사성을 모두 이야기할 수 있고, 학습과정에서 모든 node pair가 아닌 Random Walk에서 마주치는 pair들만 고려하면 되어 효율적이기 때문이다.

Unsupervised Feature Learning

Unsupervised Feature Learning에서는 Graph내에서 유사도가 높은 Node들을 Embedding에서도 가깝게 만들려고 한다. 그렇다면 u라는 Node가 주어졌을 때, 가까운 Node들을 어떻게 정의할 수 있을까?

\(N_R(u)\)를 R이라는 Random Walk 방식으로 얻은 Node u의 neighborhood라고 했을 때, 우리의 목적은 \(f:u \to \mathbb{R}^{d}:f(u) = z_{u}\)의 mapping을 구하는 것이고, 이 과정에서 얻고자하는 것은 아래와 같다.

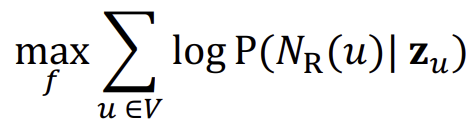
위 식에서 \(logP(N_{R}(u) \vert z_u)\)를 최대로 하는 것이 학습의 목표이다.

이를 위해 먼저 Graph내의 모든 노드 u에서 짧은 고정 길이의 Random walk를 진행하고, 이를 이용해 \(N_R(u)\)를 구한다. 이후 위의 식으로 embedding을 최적화하는 것이다.

위 식을 다르게 나타내면 아래와 같다.

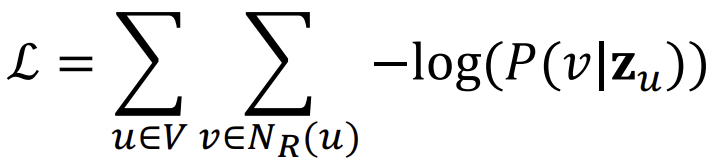
여기에 아래와 같이 softmax를 적용하면,

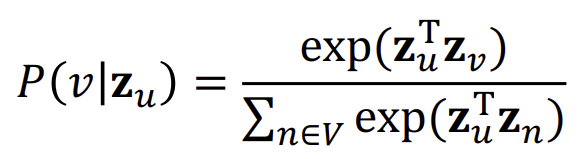
다음과 같은 최종 식이 나온다.

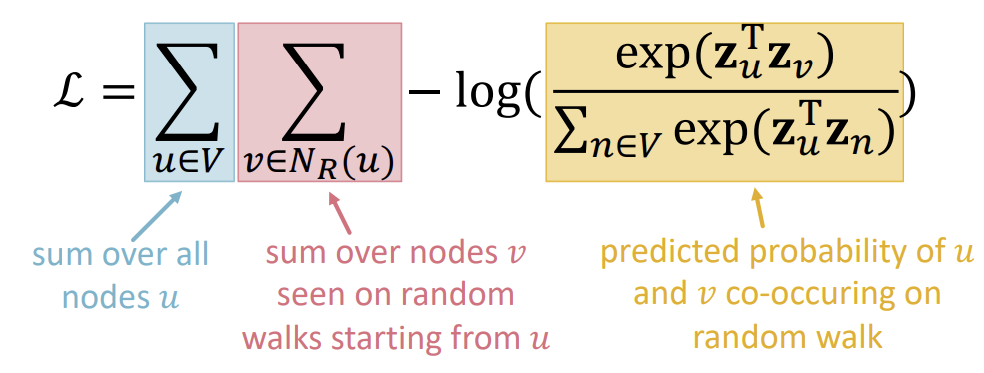
위 식에서 Random walk embedding을 최적화한다는 것은 곧 \(L\)을 최소로 만드는 \(z_u\)를 찾는 것이다. 하지만 위의 식에서 확인할 수 있듯, \(V\)에 속하는 모든 \(u\)와 \(N_{R}(u)\)에 속하는 모든 \(v\)를 확인하는 것은 \(O(\vert V \vert ^2)\)만큼의 복잡도를 가진다.

이에 대한 해결책이 Negative sampling이다.

Negative Sampling

Negative Sampling을 수식으로 설명하면 다음과 같다.

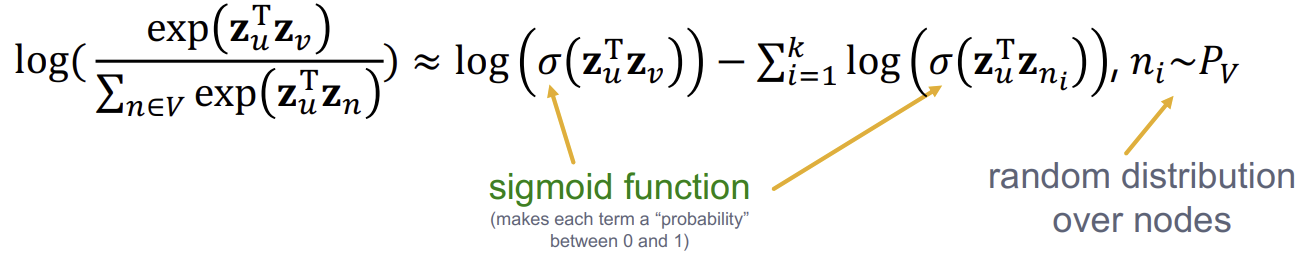
풀어 말하자면, 모든 node에 대해 normalization을 진행하는 것이 아니라, k개의 랜덤한 negative sample(해당 Node와 무관한 Node)들을 추출해 이에 대해서면 normalization을 하는 것이다.

또한 기존에 \(exp\)함수로 했던 계산을 \(\sigma\)함수로 바꾸었다.

이때, 마지막 \(n_{i} \sim P_{v}\)으로 k개를 랜덤 추출할 때는, k가 클수록 robust하지만 negative event에 대해 높은 bias를 가지게 되며, 일반적으로 k = 5 ~ 20으로 지정한다.

Stochastic Gradient Descent

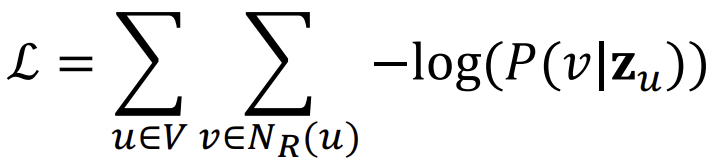
위의 objective function을 알고난 후, 이를 최소로 만들기 위해서는 Stochastic Gradient Descent 방법을 사용한다.

Stochastic Gradient Descent는 일반적인 Gradient Descent 방법과 같이 랜덤한 지점에서 시작하여 기울기를 계산하고 크기가 작은 방향으로 한 step을 이동하지만, 이때 모든 범위에 대해 기울기를 계산하지 않고, sampling한 Node에 대해서만 계산을 한다.

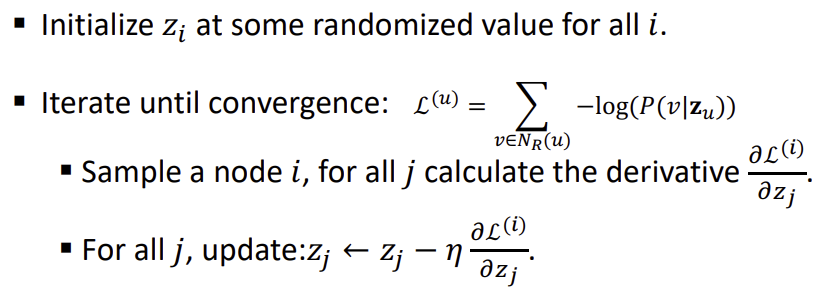
Random Walk에 대한 요약을 하자면 아래와 같다.

이렇게 고정 길이의, 완벽하게(unbiased) 랜덤한 Random Walk보다 혹시 더 좋은 방법은 없을까? 이러한 Random Walk를 더 발전 시킨 방법이 node2vec이다.

node2vec

node2vec은 biased(확률이 모두 동일하지 않은)하고, 2nd order(직전의 값을 기억하는) walk를 한다.

또한 local한 네트워크에 집중하고 싶은지, global한 네트워크의 view를 보고싶은지에 따라 BFS와 DFS를 선택한다.

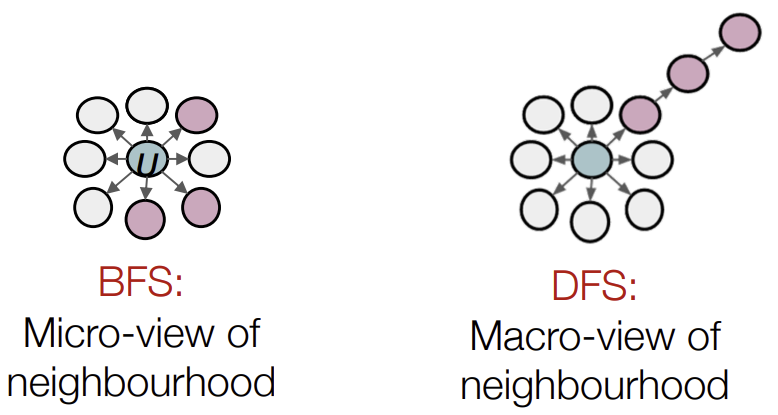
이걸 구현하기 위해 p와 q라는 2가지 파라미터를 사용한다.

• p (Return parameter) : 이전 Node로 돌아갈 확률을 정한다.
• q (In-out parameter) : BFS와 DFS의 비율을 정한다.

예를 들어, 이전에 \(S_1\) Node에서 현재 W Node로 온 경우에, \(S_2\) Node는 \(S_1\) Node로부터 W Node와 같은 거리상에 있기 때문에 BFS를 선택하는 것이고, \(S_3\) Node는 \(S_1\) Node에서부터 더 멀리로 이동하는 것이므로 DFS를 선택하는 것이라고 볼 수 있다. 그리고 \(S_1\) Node로 이동하는 것은 이전 Node로 돌아가는 것이므로 아래의 그림처럼 표현할 수 있다.

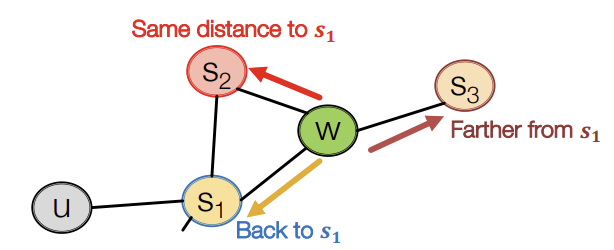
이를 구현하기 위해 위에서 언급한 파라미터 p, q는 다음과 같이 사용된다.

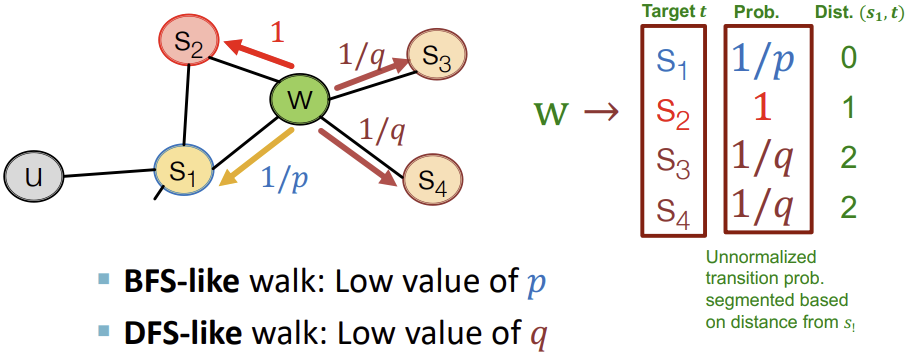
이러한 node2vec 알고리즘은 linear한 시간복잡도를 가지고 있고, 병렬 계산이 가능하다는 장점이 존재한다. 하지만 모든 Node에 대해 개별적인 embedding을 학습시켜야해서 Node의 수가 많은 경우 학습량이 많아진다는 단점 또한 존재한다.

출처, 더 궁금하다면?

Stanford CS224W: ML with Graphs | 2021 | Lecture 3.2-Random Walk Approaches for Node Embeddings