Graph-level Features

Graph-Level Feature의 목표는 전체 그래프의 구조를 나타내는 것이다. Graph-Level의 Feature에 대해 설명하기 위해선 먼저 Kernel Methods를 이해해야한다.

Kernel Methods는 Feature Vector 대신 Kernel을 Design하는 것으로, 전통적인 Graph-Level 예측을 위한 ML에 다방면으로 사용된다. 간단히 말하자면, K라는 Kernel은 두 data 사이의 유사도 값이고, \(K(G,G’) = \phi(G)^{T}\phi(G’)\)에서 \(\phi(G)\)는 G에 대한 Feature이다. 이러한 Kernel들로 Kernel Matrix를 만드는데, 이는 Graph내의 모든 pair에 대한 유사도 정보를 담고있다. 이때, Kernel Matrix는 양수의 eigenvalue를 가지고, 대칭이다. 이렇게 Kernel이 정해지면, 해당 모델은 즉시 예측에 사용될 수 있게 된다.

아래는 Kernel에 대한 자세한 설명이다.

Graph Kernel : Key Idea

Graph Kernel의 목적은 feature vector \(\phi(G)\)를 Design 하는 것이다. 이때 Bag-of-Words(BoW) 기법을 기반으로 사용하는데, BoW는 단순히 Document 내의 각 단어 갯수를 feature로 사용하는 방식이다.

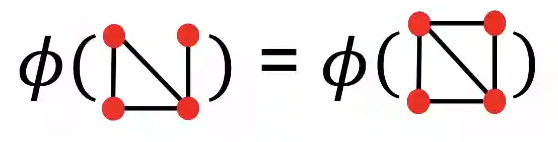
이를 Graph에 적용할 때, 위의 그림처럼 Node의 수를 센다면, 4개의 Node를 가진 Graph는 모두 같은 feature를 가져 문제가 생긴다. 이를 해결하기 위해 Node의 Degree를 사용하는 방법이 고안되었다.

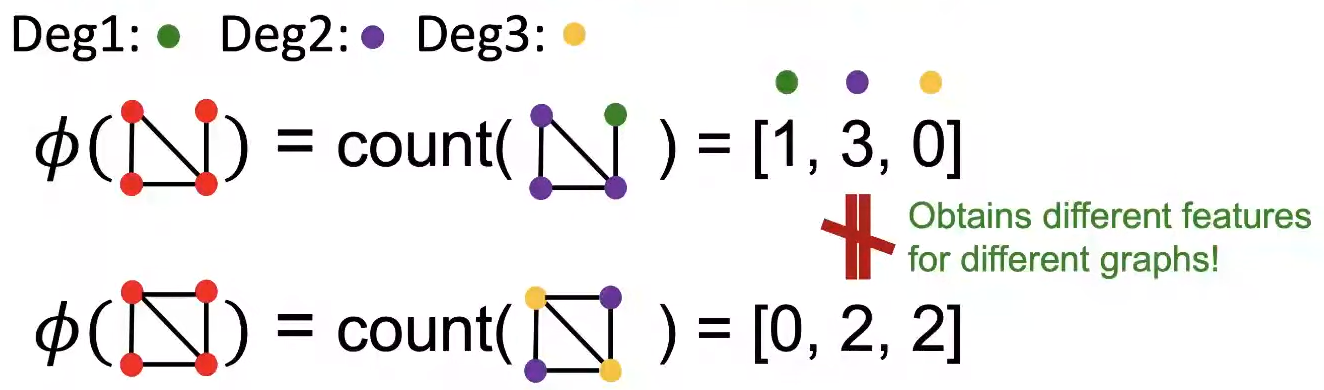
위의 그림과 같이 Node의 Degree를 feature로 사용하는 경우, Node를 사용했을 때 같은 feature를 가졌던 Graph들이 다른 feature를 갖게 되어, feature가 전체 Graph에 대해 더 잘 설명하게 된다.

이처럼 Graph 전체에 대해 더 많은 정보를 담을 수 있는 feature를 만드는 것이 Graph-Level의 ML에서 중요하다. 그렇다면 Node Degree를 사용하는 방식보다 더 좋은 방식은 없을까?

Graphlet Features

Node Degree의 수보다 조금 더 구체적인 요소를 feature로 사용하는 방법은 Graphlet을 사용하는 방법이다. 이는 Graph 내의 서로 다른 graphlet의 개수를 세는데, 이때 graphlet은 서로 연결되지 않아도 되고, rooted(Graphlet 내에서 Node의 위치가 정해진)되지 않아도 된다.

아래는 이해를 돕기위해 Graph의 Node 수가 3, 4인 경우에서, 서로 연결되지 않아도 되고 unrooted한 Graphlet들을 나타낸 그림이다.

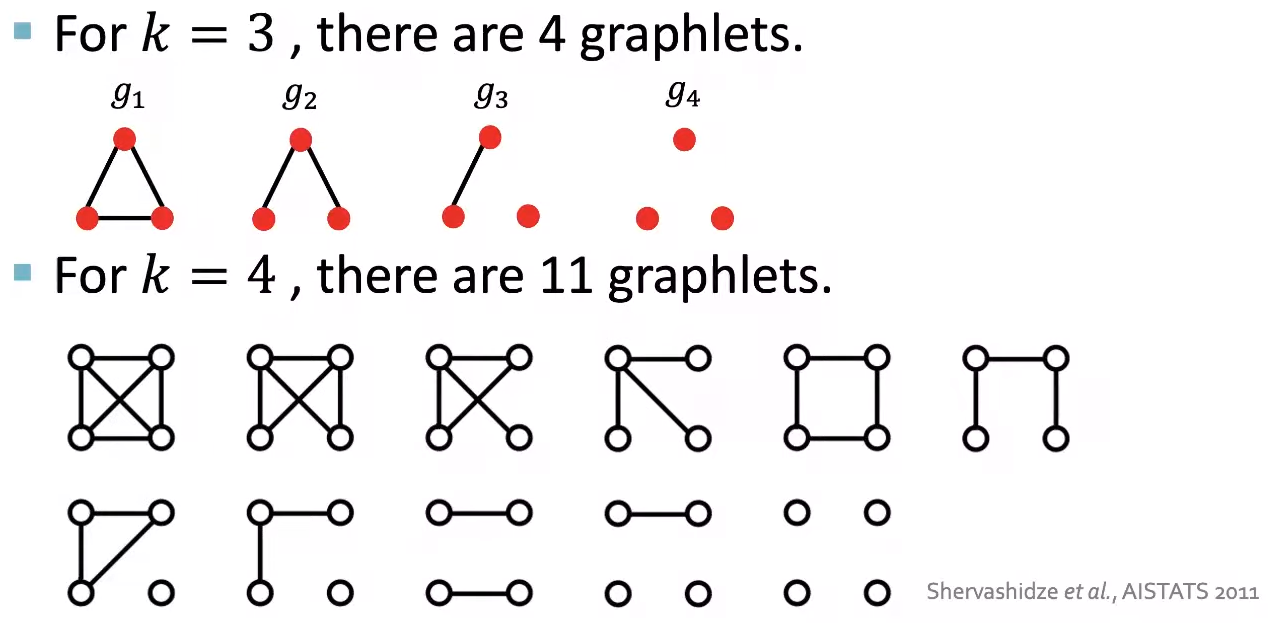
Graphlet feature을 사용할 때는, 주어진 Graph에서 정해진 크기의 Graphlet들의 개수를 세어 아래 그림처럼 vector로 나타낸다.

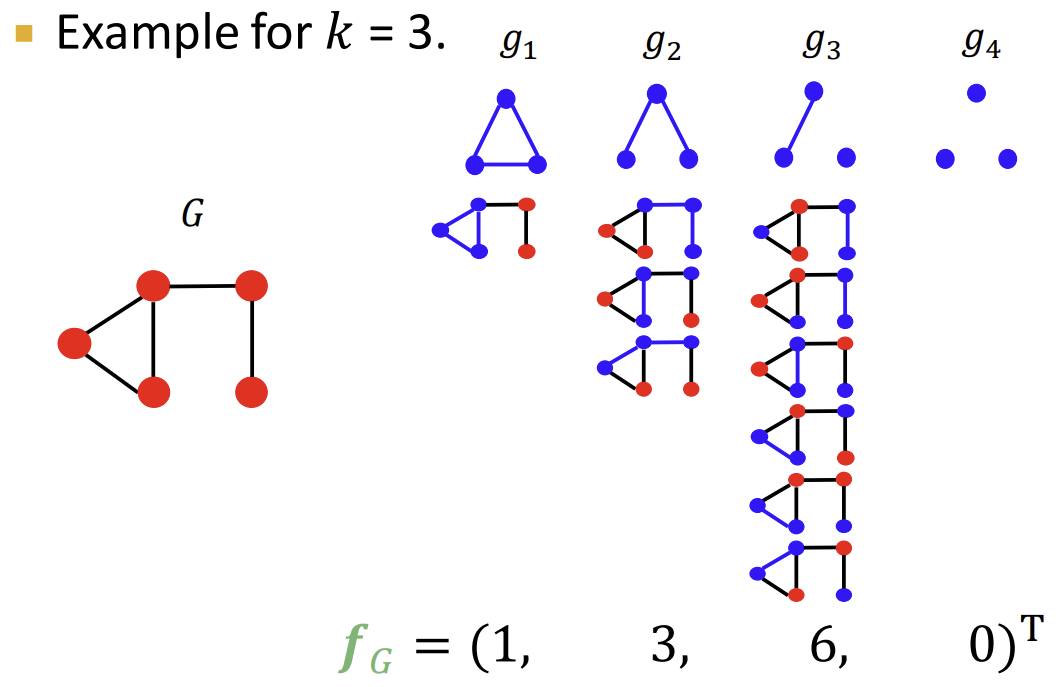
이렇게 구한 vector를 위에서 언급했던 \(\phi(G)\)로 사용하여, 두 그래프의 Graphlet vector를 normalize하여(그래프의 크기가 다르면 곱연산이 불가능하기 때문.) 곱연산을 한다. 그러면 \(K(G,G’) = \phi(G)^{T}\phi(G’)\)의 형태가 되며, 이렇게 구한 K를 두 Graph의 유사도 feature로 사용하는 것이다.

아래는 normalize 하는 방법에 대한 설명이다.(여기서는 \(\phi(G)\)대신 \(f_G\)로 나타내었다.)

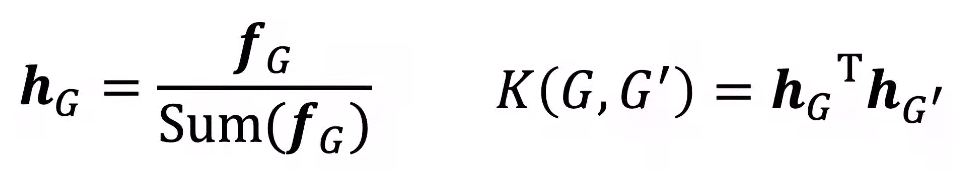
이렇게 Node Degree의 단점을 극복한 Graphlet 방식도 완벽하지는 못하다. 그중 가장 큰 단점은 바로 시간복잡도이다. 크기가 \(n\)인 Graph에서 크기가 \(k\)인 Graphlet의 수를 세는 task는 \(n^k\)의 시간복잡도를 가진다. 이러한 문제는 subgraph isomorphism test가 NP-hard 문제이기 때문에 해결이 불가능하다. 그나마 괜찮은 해결책은 Graph 자체의 Node Degree를 \(d\)로 작게 한정하면 \(O(nd^{k-1})\)로 괜찮은 효율을 내는 알고리즘을 만들 수 있다.

그렇다면 좀 더 효율적인 Graph Kernel을 Design할 수는 없을까?

Weisfeiler-Lehman Kernel

Weisfeiler-Lehman Kernel은 Graphlet을 사용한 방법보다 더 효율적인 feature descriptor(\(\phi(G)\))를 찾는 것을 목표로 한다.

이 방법은 기존에 one-hop neighborhood 정보만을 지녔던 Bag-of-NodeDegrees를 일반화하여 multi-hop neighborhood에 대한 정보를 지닌 feature를 사용한다. 이러한 방법을 사용하기 위해 Color refinement라는 알고리즘을 사용한다.

Color Refinement

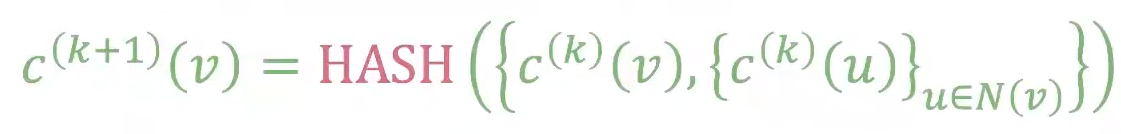
위는 Color Refinement 알고리즘을 한번에 나타낸 공식이다. K step이 지난 후, \(c^{(K)}(v)\)가 K-hop neighborhood의 구조를 요약하는 정보를 담게 된다.

공식으로만 이야기하면 직관적으로 이해하기 힘드니 그림으로 설명해보도록 하겠다.

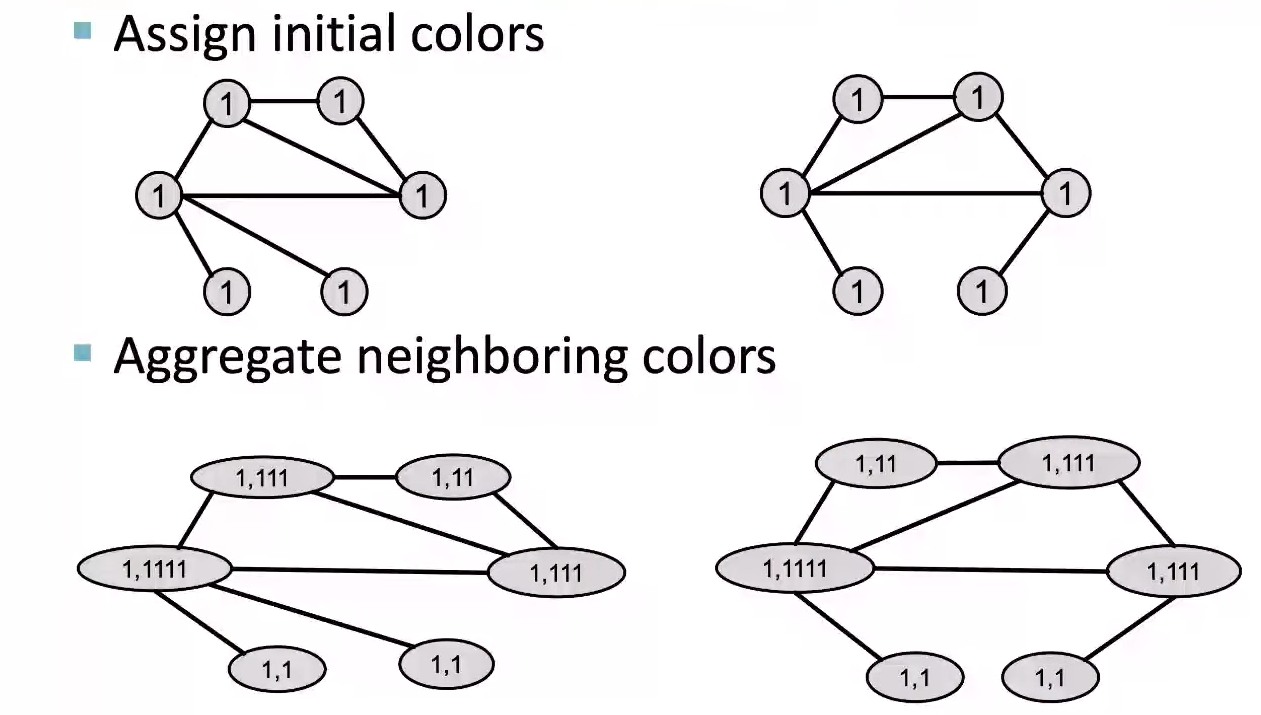
먼저 각 Node에 초기 색을 부여한다. 여기서는 첫 step이기 때문에 모든 Node들이 같은 색을 가지고 있다. 이후 neighbor Node들의 색을 aggregation(vector를 연장함)한다.

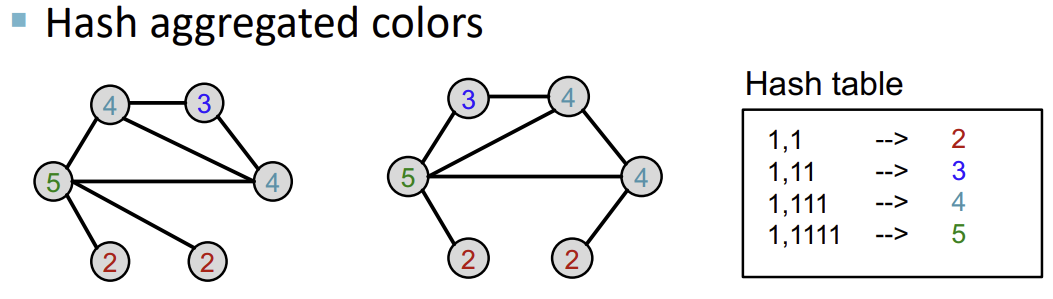
다음으로, 생성된 vector를 Hash table을 통해 특정 색으로 mapping한다.

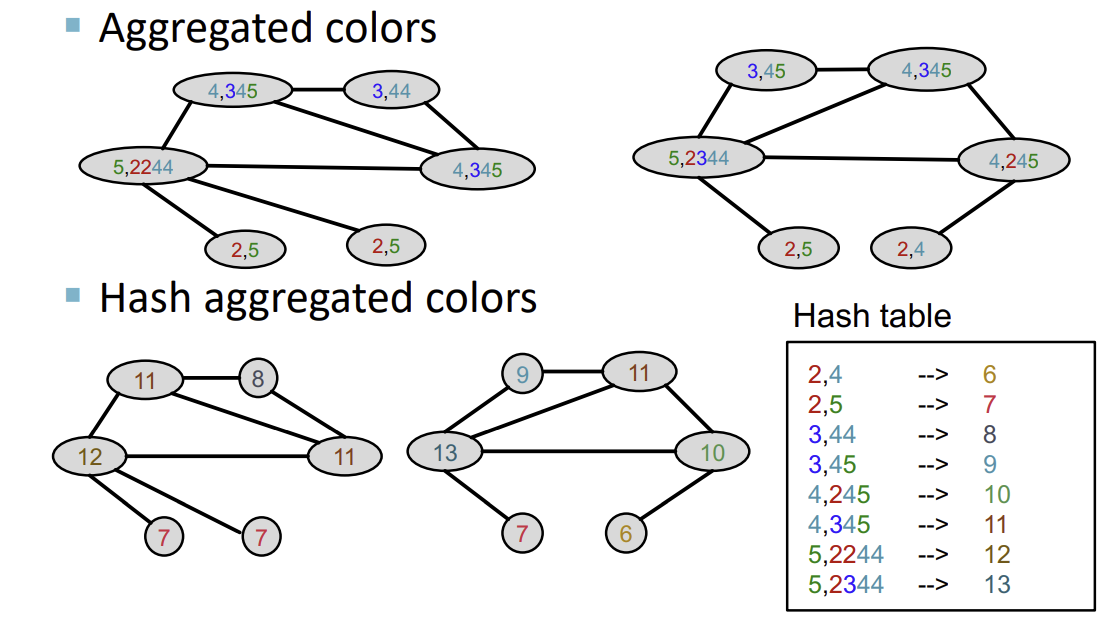
이후의 과정들은 위의 반복이다. 또다시 neighbor Node들의 색을 aggregation하고, 이를 Hash table을 이용해 mapping한다.

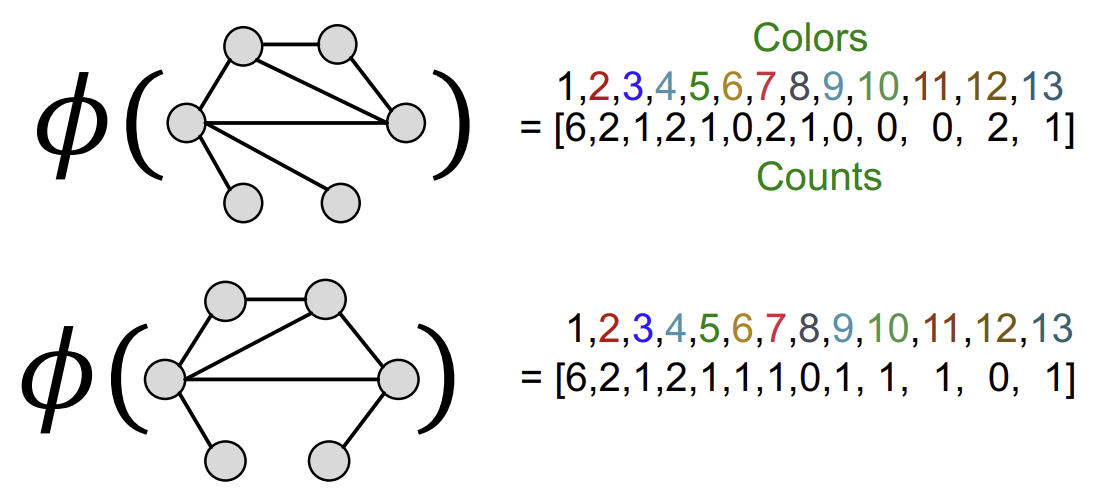
지정한 K-step을 모두 완료하면, 해당 Graph에 존재하는 색들의 개수를 세어 vector로 만든다. 이 vector가 바로 Weisfeiler-Lehman Feature이다.

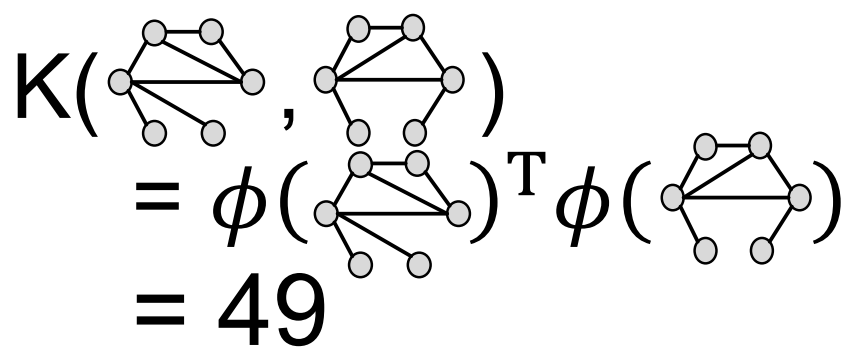
이후 위에서 설명했던 \(K(G,G’) = \phi(G)^{T}\phi(G’)\) 형태의 공식을 통해 두 Graph의 유사도를 구한다.

위에서 언급했듯, 이 방식은 Node의 수에 대해 linear한 시간복잡도를 가져 계산이 굉장히 효율적이다. 또한 각 단계에서 메모리에 각 Node의 색만 저장하면 되고, 최악의 경우 색의 수는 node의 수와 같으므로 메모리 또한 많이 사용하지 않는다. 따라서 전체 복잡도 또한 Node 수에 linear하다.

Graph-Level Features: Summary

2강 Summary

출처, 더 궁금하다면?

Stanford CS224W: ML with Graphs | 2021 | Lecture 2.3 - Traditional Feature-based Methods: Graph