Link-level Task and Features

Link-level의 ML 학습은 존재하는 Link들을 토대로 새로운 Link를 예측하는 목적을 지닌다. test시 Link가 존재하지 않는 모든 Node pair들에 순위를 매기고, 상위 K개 Node pair에 새로운 Link가 있을 것이라고 예측한다.

이러한 ML 학습을 위해 Node1번과 Node2번의 feature를 합연산하여 계산할 수도 있겠지만, 그런 경우 많은 정보 손실이 발생할 것이므로, Node pair에 대한 feature를 design해야 한다.

Link Prediction에는 2가지 종류가 있다.

먼저 Random하게 Link가 missing하는 경우에는 학습시키는 과정에서 Random하게 Link들을 삭제하고 이를 예측하도록 한다. 이는 변화하지 않는 static-network, 예를들어 단백질 간의 상호작용 등에 사용될 수 있다.

다른 한가지 종류는 시간이 지날수록 변화하는 네트워크에 대해 이전 시간의 Graph를 주고 미래 시간에 새로 생겨날 Link를 찾아내는 방식이다. 이는 시간에 따라 변화하는 Social Network와 같은 evolving-network에 사용된다.

Link Prediction via Proximity

확률을 통한 Link 예측을 할 땐, 모든 (x,y) Node pair에 대해 score c(x,y)를 계산한다. 이후 score를 정렬하여 상위 n개를 새로 나타날 Link로 예측하고, 예측값이 맞는지 실제 나타나는 Link들과 비교한다.

Link-Level Featrues

Overview

Link-Level Feature는 크게 3가지로 나눌 수 있다.

• Distance-based feature
• Local neighborhood overlap
• Global neighborhood overlap

Distance-Based Features

Distance-Based Feature의 대표적인 것으로는 Shortest-path distance between two nodes 즉, 두 Node 사이의 최단거리를 활용하는 방법이 있다.

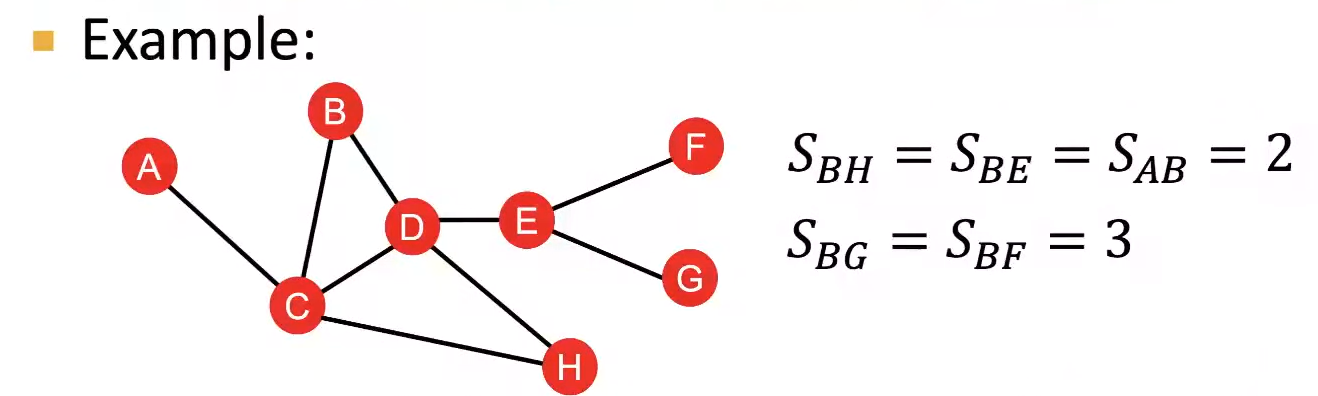
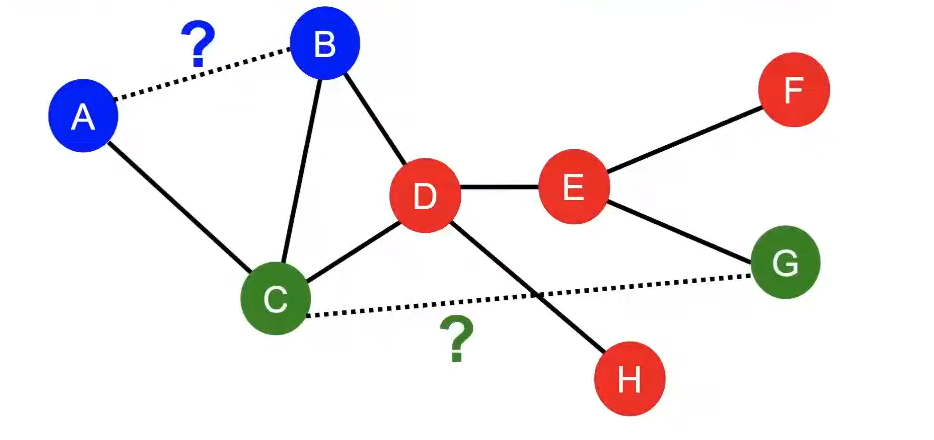
이 방식은 Neighborhood overlap의 degree 즉, 두 Node가 공유하는 Neighbor의 수를 고려하지 못해 Connection의 강함을 비교할 수 없다. 예를들어 위 예제에서는 B와 H가 더 많은 이웃을 고려하므로 다른 거리가 2인 관계들보다 더 강한 Connection을 가지지만, 최단거리 방식으로는 이를 알 수 없다.

Local Neighborhood Overlap

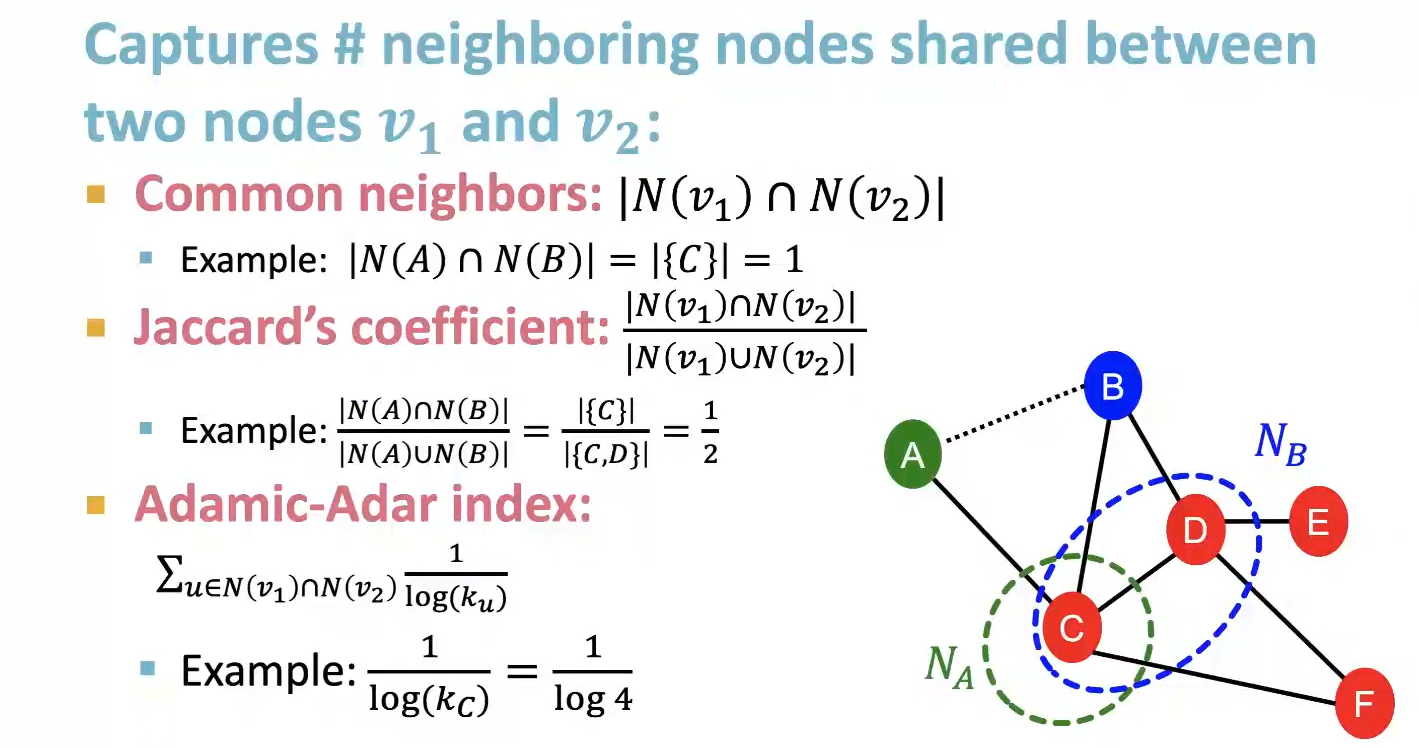
1. Common Neighbors

첫번째 방식인 Common neighbors 방식은 단순히 Node v1과 v2의 공유 이웃의 개수를 사용하는 방식이다. 하지만 이 방식에서는 이웃의 수가 많은 Node가 큰 값을 가지게 된다는 허점이 존재한다.

1. Jaccard’s Coefficient

두번째 방식은 v1과 v2의 공유 이웃 수를 v1과 v2 각각의 이웃 수 합으로 나눈 값을 사용하는 것이다. 이를 통해 이웃이 많은 Node에 손해를 주어 첫번째 방법의 문제를 해결하였다.

1. Adamic-Adar Index

마지막 방식은 모든 교집합 노드에 대해 교집합 Node Degree의 로그 역수값을 모두 합하는 것이다. 이 방식은 Degree가 낮은 공유 이웃이 많으면 유리하고, Degree가 낮은 이웃이 많으면 손해를 본다. 이 방식은 이웃의 이웃과 새로운 Link를 생성하는 경우가 잦은 Social-Network에서 잘 사용된다.

하지만 이 방식들 또한 단점을 가지고 있다. 바로 공유 이웃이 없으면 상대적으로 가까운 pair이던 먼 pair이던 0의 값을 가진다는 것이다. 이를 해결하기 위해 Global neighborhood overlap 방식을 사용하여 전체 Graph를 고려한다.

Global Neighborhood Overlap

Global Neighborhood Overlap에서는 Kats index를 사용한다. 이는 두 Node 사이의 모든 길이의 Path를 count 하는 방식으로, 계산복잡도가 높을 것 같지만, 1강에서 배운 Adjacency matrix를 사용하면 간단하게 계산할 수 있다.

위 사진은 길이가 2인 Path의 수를 Count 하는 방법을 설명하고 있다. 먼저 u에서 v로의 Path라고 가정하면, u의 Neighbor들과 v 사이의 Path를 계산한다. u에서 u의 Neighbor에게 가는 Path는 길이가 1이고 하나 뿐일 것이므로, 이 값들을 모두 합하면 u에서 v까지 가는 모든 path의 수를 구할 수 있게 된다.

이렇게 모든 Path를 더할 때, 길이가 긴 Path일수록 weight를 적게 부여하여 feature값을 계산한다. 아래의 공식은 위 공식을 closed-form으로 표현한 것이다.

Link-Level Features: Summary

출처, 더 궁금하다면?

Stanford CS224W: ML with Graphs | 2021 | Lecture 2.2 - Traditional Feature-based Methods: Link