2장 개요
Machine Learning Tasks
전통적 ML pipeline은 현대의 딥러닝과 달리 사람이 직접 feature를 설정해준다.따라서 전통적 ML 방식에서는 feature를 제대로 디자인 하는 것이 가장 중요하다. 좋은 feature는 Graph의 구조를 잘 표현하고 Node의 attribute/property를 잘 표현해야한다.
이번 2장에서는 구조적 feature, 즉 한 Node 근처의 네트워크 구조와 전체 그래프의 구조를 표현하는 feature에 집중하여 알아보고자 한다. 2강은 아래의 3단계로 구분지어 진행된다.
- Node-level prediction : node를 설명하는 feature
- Link-level prediction : pair of nodes를 설명하는 feature
- Graph-level prediction : 전체 그래프의 topology를 설명하는 feature

Node-level Tasks and Features
Node-level의 ML 학습은 semi-supervised 형식으로 진행된다. 예를들어 Graph내에서 몇가지 Node들은 색을 알려주고, 색을 알려주지 않은 Node들의 색을 예측하는 식의 방식이다.
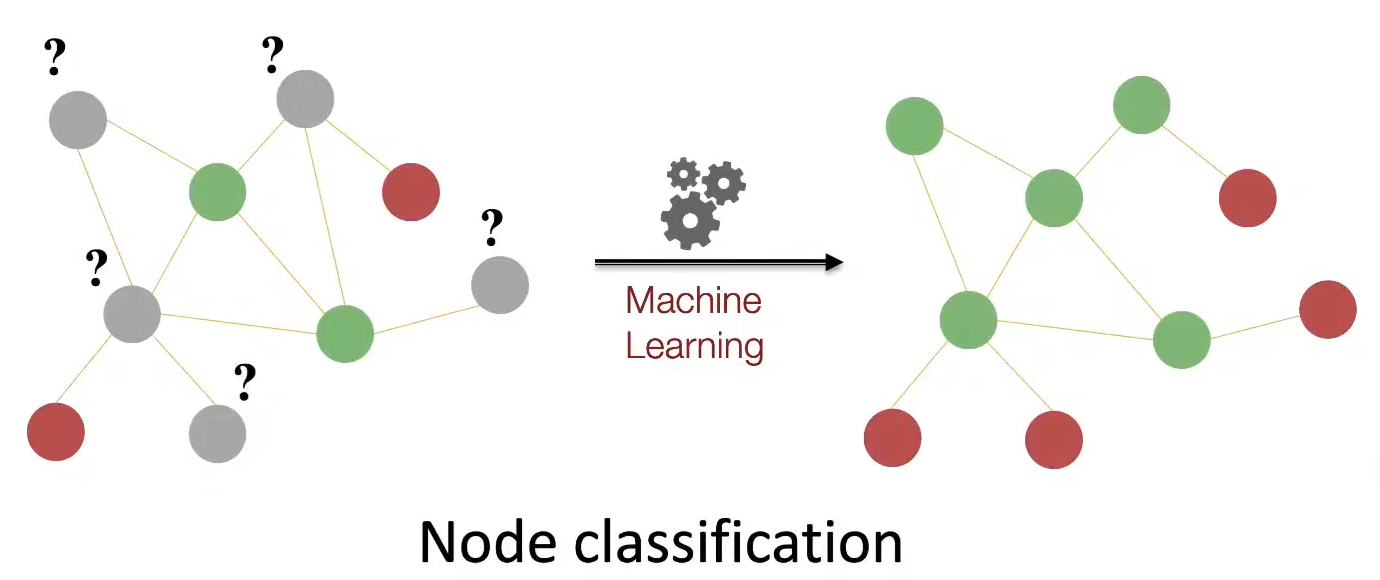
Node-Level에서의 goal은 각 Node의 구조와 position정보를 feature로 설명하는 것이다.
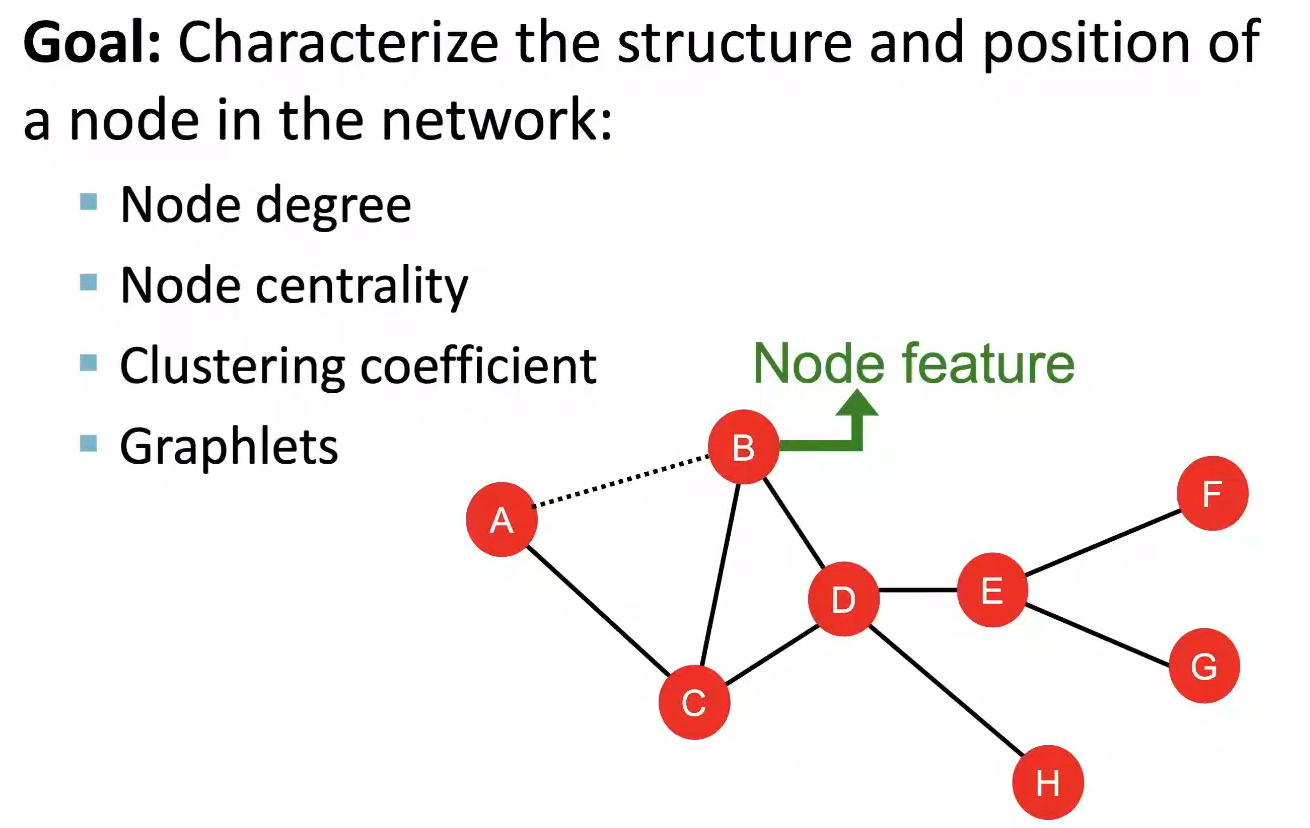
Node Featrues : Node Degree
이미 이전 강의에서 배운 Node Degree를 feature로 활용하는 건 어떨까? Node Degree는 얼마나 많은 이웃들을 가졌는지에 대한 정보는 담고있지만, 이웃의 특성이나 누구와 Link를 이루고 있는지에 대한 positional 정보는 고려하지 못한다.
Node Featrues : Node Centrality
그래서 Node Degree의 단점을 해결할 수 있는, Graph 내에서 해당 Node의 중요도를 측정하는 방식이 Node Centrality이다. 이번 시간에 배울 Node Centrality는 아래의 3가지이다.
- Eigenvector Centrality
- Betweenness Centrality
- Closeness Centrality
Eigenvector Centrality
Eigenvector Centrality는 한 Node가 중요한 Node들을 neighbor로 가지고 있다면 그 Node 또한 중요할 것이라는 가정 하에 만들어졌다.
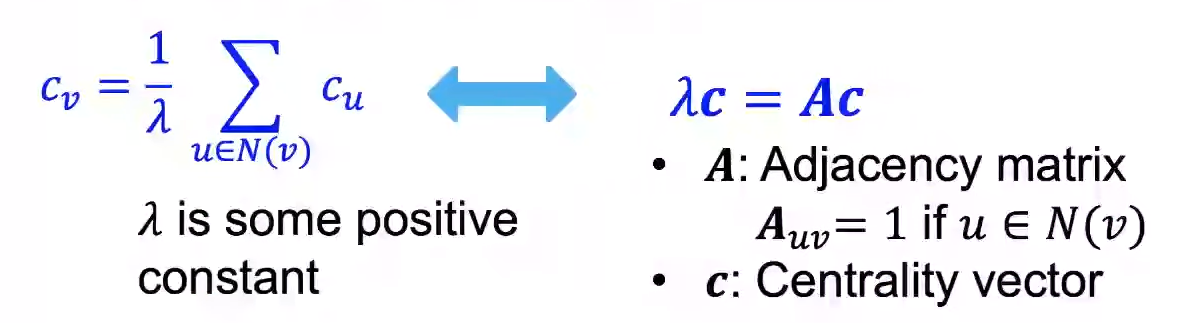
\(lambda_{max}\)는 항상 양수이며 고유하며, leading eigenvector \(c_{max}\)는 centrality를 위해 사용된다.
Betweenness Centrality
Betweenness Centrality는 다른 Node들 간의 최단거리 path에 해당 Node가 자주 포함되는 경우, 그 Node를 중요하다고 가정한다. 따라서 아래 공식과 같이 해당 Node(v)를 제외한 두 Node들 사이의 최단거리 path들 중에서 v가 포함되는 path의 수를 모두 더하여 계산한다. 이 방법을 통해 Node가 네트워크 내에서 얼마나 중요한 connector인지를 판단할 수 있게 된다.
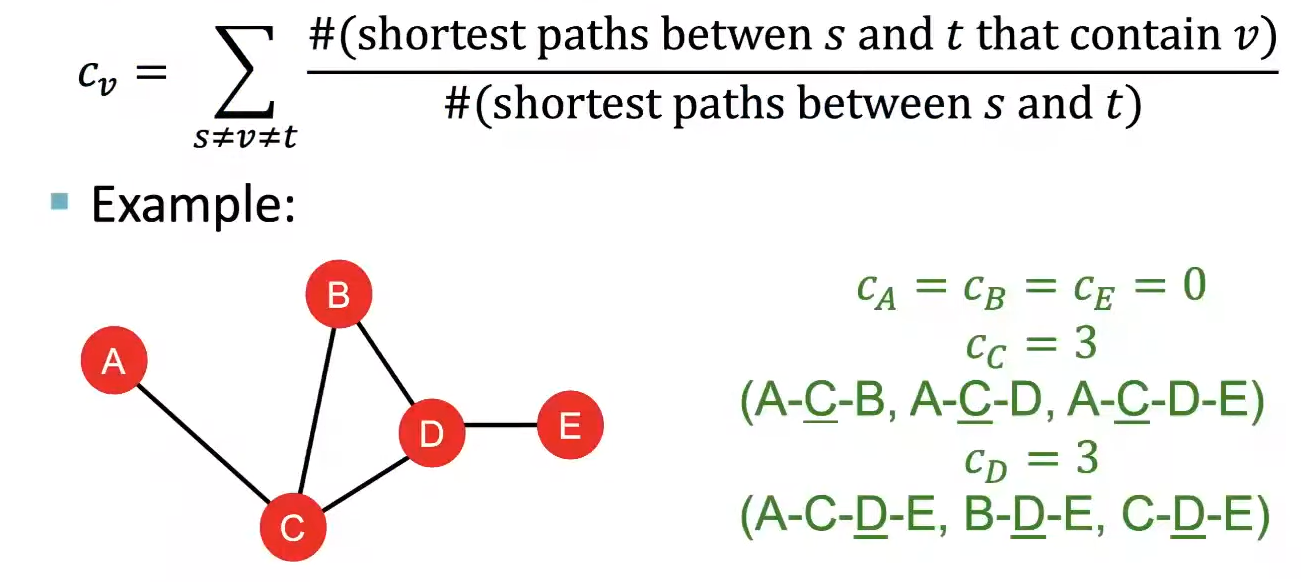
Closeness Centrality
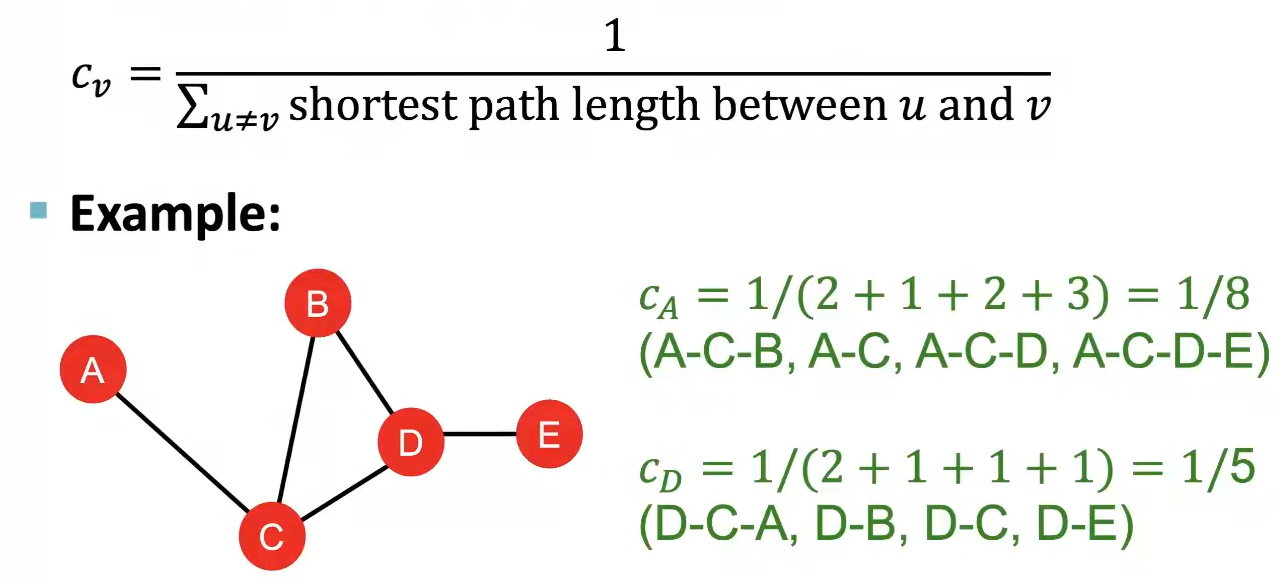
Colseness Centrality는 해당 Node에서 다른 모든 Node들까지의 최단거리 합이 짧을수록 중요한 Node라고 가정한다. 따라서 아래 공식처럼 최단거리 합을 역수로 하여 feature로 사용한다.
Node Features : Clustering Coefficient
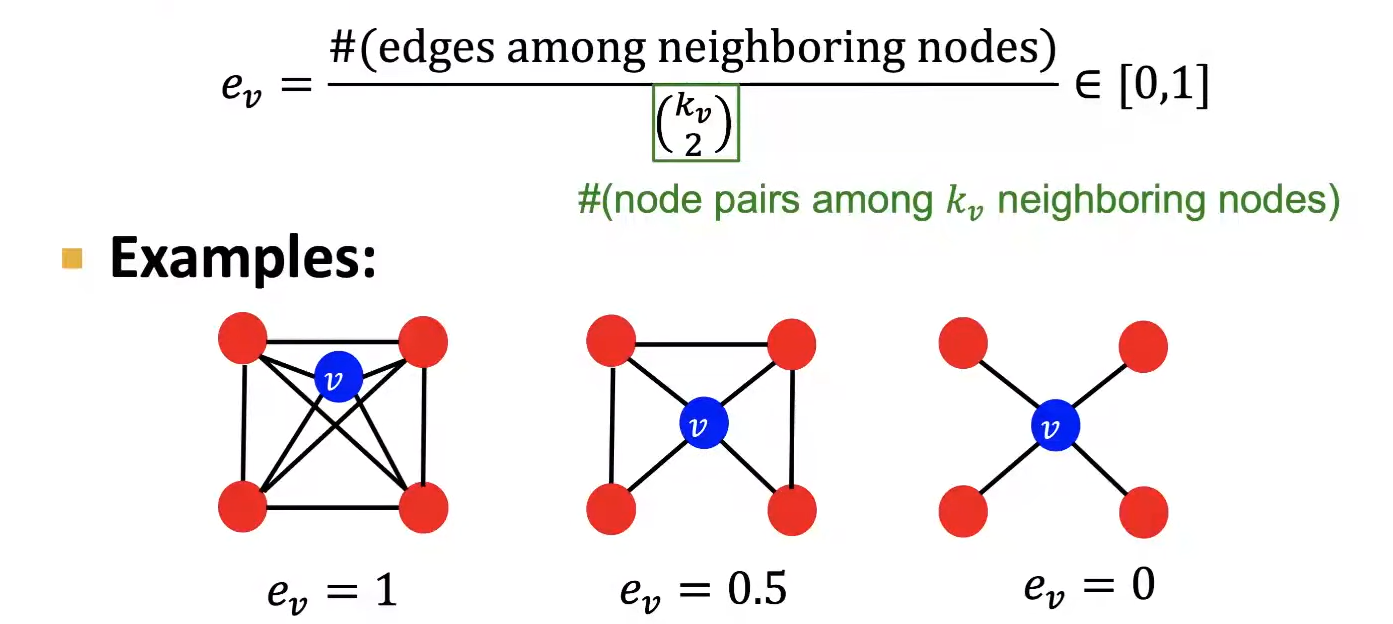
위에서 본 Centrality가 한 Node가 Graph내에서 얼마나 중요한지를 판단하는 feature였다면, Clustering Coefficient는 Local Structure를 판단하는 feature이다. 아래 공식에서 확인할 수 있듯, 계산 방식은 Neighbor Node들로 만들어질 수 있는 pair을 분모로 하고, 실제로 존재하는 Edge의 수를 분자로 한다. 따라서 [0,1]의 범위를 가지는 feature이다.
Node Features : Graphlets
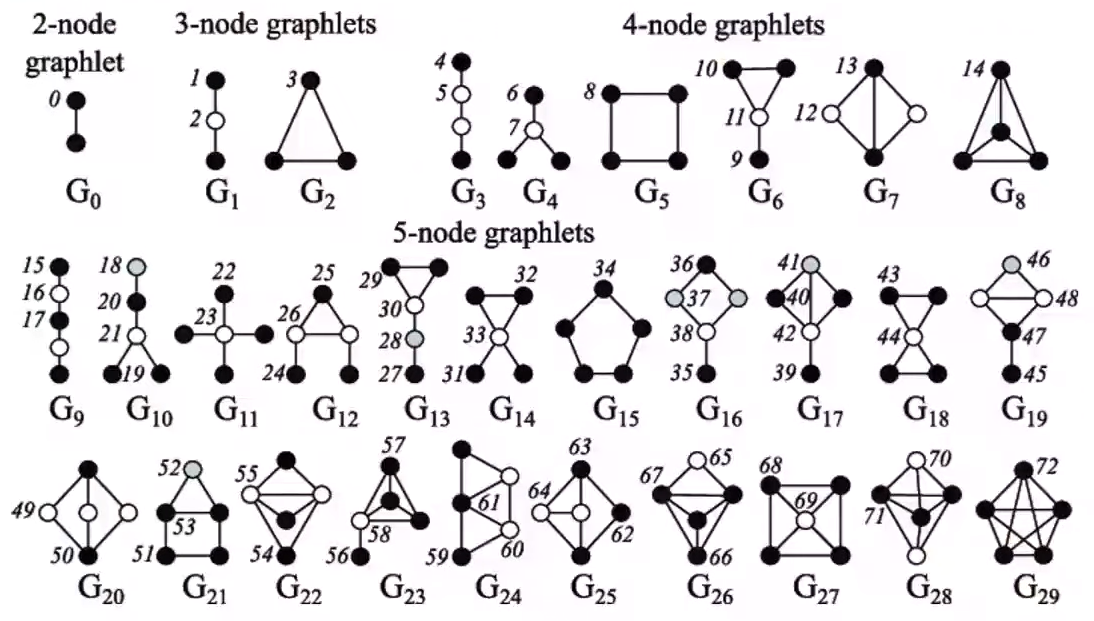
Graphlet은 Subgraph의 종류라고 볼 수 있다. 하지만 이때, non-isomorphic(형태가 같지 않다)하고, Rooted(Subgraph 내의 위치를 고려)하다. 아래의 그림은 2-node ~ 5-node의 모든 Graphlet을 보여주고 있다.
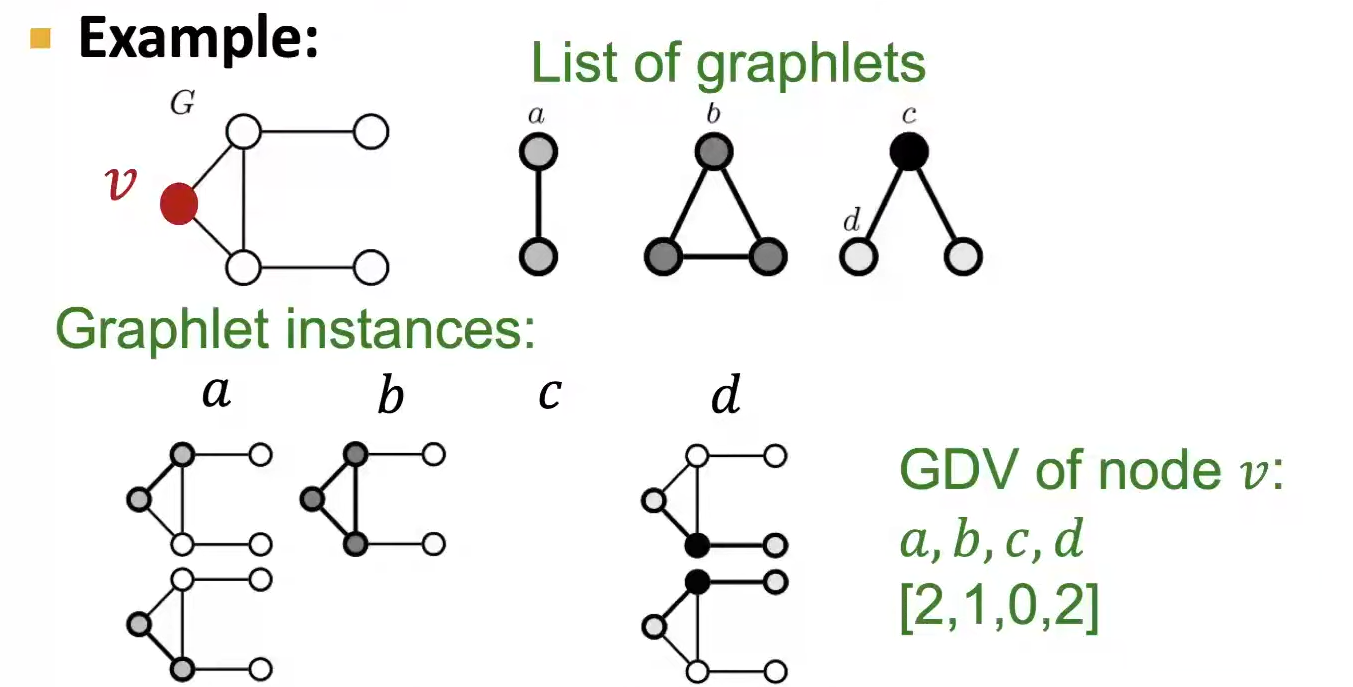
Graphlet Degree Vector(GDV)는 Node에 대한 Graphlet 기반의 feature이다. 이는 Node가 속한 Graphlet의 개수를 종류별로 Vector에 저장한다. 따라서 자신을 포함하여 거리가 4인 Node(4 hop)까지의 구조를 위의 Graphlet 목록에 의하면 73차원 Vector로 표현할 수가 있는 것이다. 이를 통해 해당 Node 주변의 Local Network Topology의 정보를 feature로 나타낼 수 있다.
아래는 3-node까지의 GDV의 예시이다.
Node-Level Features: Summary

출처, 더 궁금하다면?
Stanford CS224W: ML with Graphs | 2021 | Lecture 2.1 - Traditional Feature-based Methods: Node