GNN Training Pipeline

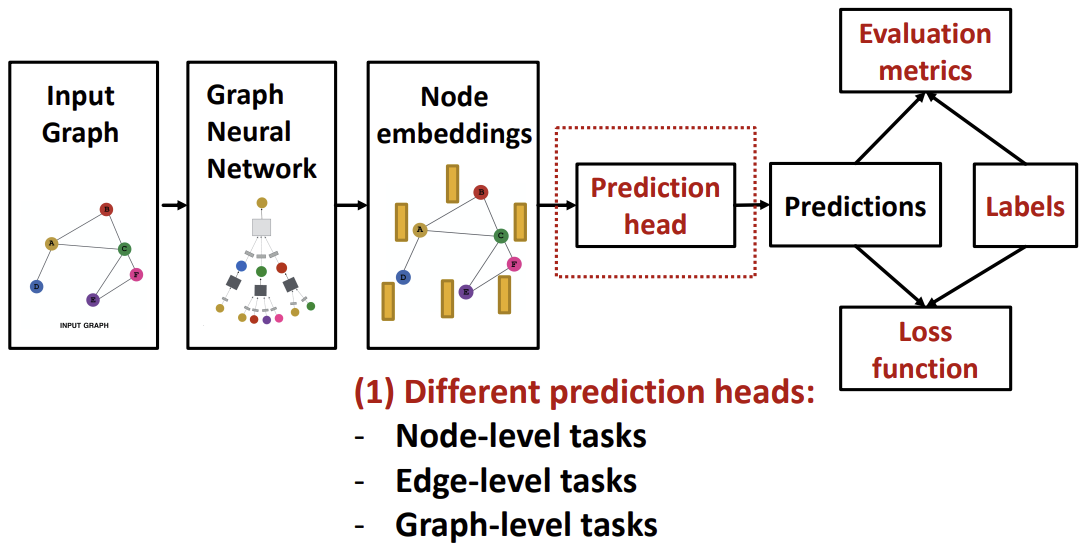
이전 강의들에서 위 그림에서 좌측 부분의 Input Graph, Graph Neural Network, Node Embeddings에 대해 다루었다. 이번 강의에서는 우측의 본격적인 GNN Training 부분을 배워보고자 한다.

GNN Prediction Heads

Prediction Head는 final node의 output을 의미하며, node/link/graph level의 task level에 따라 다른 prediction head가 존재한다.

Prediction Heads : Node-level

Node level에서는 Node 임베딩을 이용해 바로 prediction을 할 수 있다. 아래 그림의 \(h\)는 GNN의 계산을 마친 후의 d차원의 노드 임베딩이고, 이를 그대로 k차원의 행렬 \(W^{(H)}\)에 곱하여 예측값인 \(\hat y_{v}\)을 얻는다. 이 결과로 k-way prediction(Classification, Regression 등)의 Prediction Head를 구할 수 있다.

Prediction Heads : Edge-level

Edge-level의 경우, Node 임베딩 pair로 prediction을 한다.

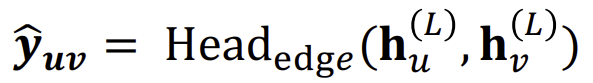
이 때의 연산인 \(Head\)를 다음과 같이 나눌 수 있다.

• Concatenation + Linear

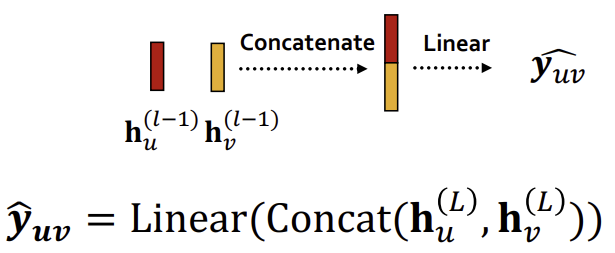
이때, Linear 연산을 통해 k차원 임베딩으로 변환을 할 수 있다.

• Dot product

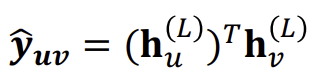
Dot product를 이용한 연산시, k-way prediction을 위해 학습 가능한 matrix \(W\)를 곱한 후 concat 연산을 추가적으로 수행한다.

Prediction Heads : Graph-level

Graph-level prediction은 그래프 내의 모든 Node 임베딩을 사용한다.

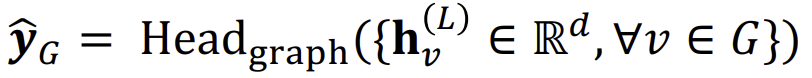
Graph-level에서도 다양한 함수를 \(Head\)로 사용할 수 있다.

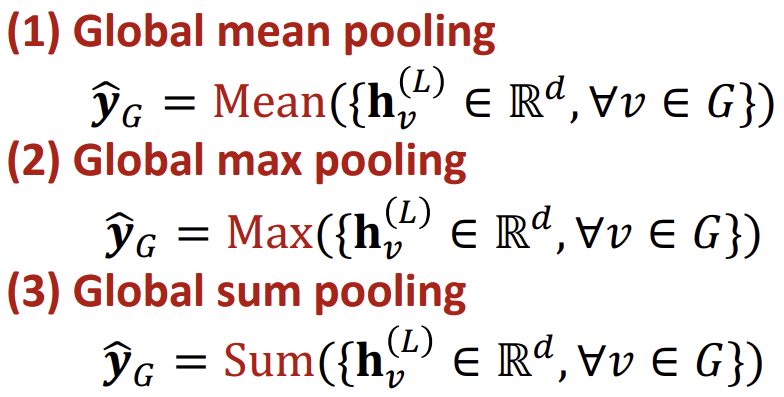
이러한 함수를 사용할 경우, 작은 그래프에서는 잘 동작할지 모르지만, 큰 그래프에서는 문제가 발생한다.

\(G_{1} : \lbrace -1,-2,0,1,2 \rbrace \)와 \(G_{2} : \lbrace -10,-20,0,10,20 \rbrace \)인 두 Node 임베딩이 존재할 때, Mean이나 Sum을 사용하면 두 임베딩의 차이를 구분할 수 없게 된다.

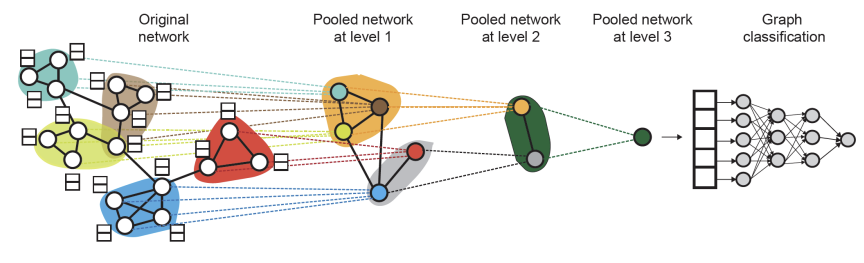
이를 해결하기 위해 Hierarchical Global Pooling을 사용한다. 이는 Pooling을 한번에 하는게 아니라 sequential하게 진행하는 방식이다. 아래의 예시에서는 먼저 앞 2개와 뒤 3개의 임베딩을 pooling하고, 결과로 나온 2개의 임베딩을 다시 pooling하고있다. 추가적으로 단순히 Sum하는 것이 아닌, non-linear함수인 ReLU를 추가한 pooling 방식을 사용하고 있다. 이를 통해 \(G_{1}\)과 \(G_{2}\)를 구분할 수 있게 되는 것을 확인할 수 있다.

그렇다면 pooling을 하는 순서를 어떻게 정해야 할까?

DiffPool에서는 이를 다음과 같이 해결한다. 2개의 GNN을 이용하여 GNN A는 임베딩을 계산하고, GNN B는 Graph를 클러스터링하여 pooling할 집합을 만드는 것이다. 이를 반복하여 최종 Node 한개만 남을 때까지 클러스터링, Pooling을 반복한다.

이때 GNN A와 GNN B의 연산이 병렬적으로 처리 가능하다는 장점이 있다.

Predictions & Labels

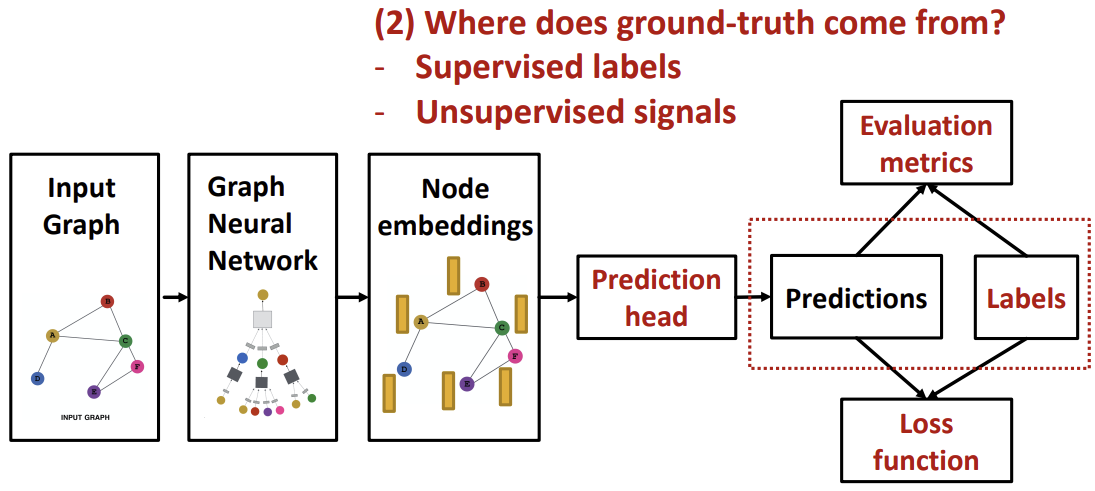
다음으로는 Prediction을 위한 label에 대해 알아보자. Label을 prediction할 때는 Supervised learning과 Unsupervised learning에 따라 방식이 나뉜다.

Supervised learning의 경우, ground-truth label이 주어진다.

하지만 unsupervised(self-supervised) learning의 경우, 외부 label 없이 그래프의 구조만을 활용하여 supervision signal을 찾아야한다.

Loss Function

Loss function은 Classification과 Regression에 따라 나뉜다. Classification의 경우, 레이블이 discrete한 값을 가지고, Regression의 경우에는 continuous한 값을 가진다.

Classification Loss

Classification Loss의 경우에는 대표적으로 Cross Entropy가 사용된다. 공식을 보면 실제값이 0에 가까운 경우에는 작은 값, 1에 가까운 경우에는 큰 값으로 예측을 해야 Cross Entropy가 최소가 된다.

Regression Loss

Regression Loss의 경우, Mean Squared Error(L2 Loss)를 많이 사용한다. MSE는 실제값과 예측값의 차를 제곱하여 합하는 방식을 사용한다.

Evaluation Metrics

마지막으로 Evaluation Metrics에 대해 알아보자.

Evaluation Metric 또한 Regression과 Classification에서 나뉜다.

Evaluation Metrics : Regression

Regression의 경우, RMSE, 혹은 MAE를 주로 사용한다.

Evaluation Metrics : Classification

Classification은 Multi-class의 경우에는 기본적은 accuracy를 사용한다.

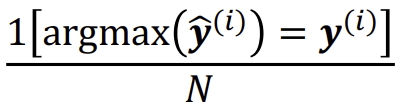
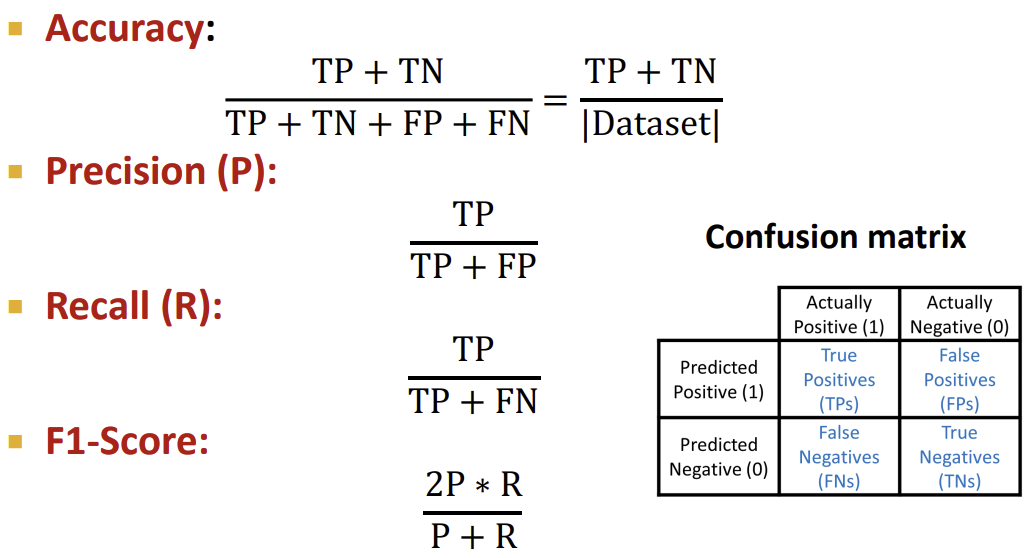
하지만 Binary Classification의 경우에는 여러 방법이 존재한다. 먼저 위에서 본 Accuracy를 사용하는데, Accuracy의 경우 데이터의 밸런스가 잘 잡혀있지(레이블이 골고루 있지) 않으면 제대로 된 결과값이 나오지 않는다. 따라서 Precision/Recall, 그리고 이 둘을 합친 F1-Score를 사용할 수 있다.

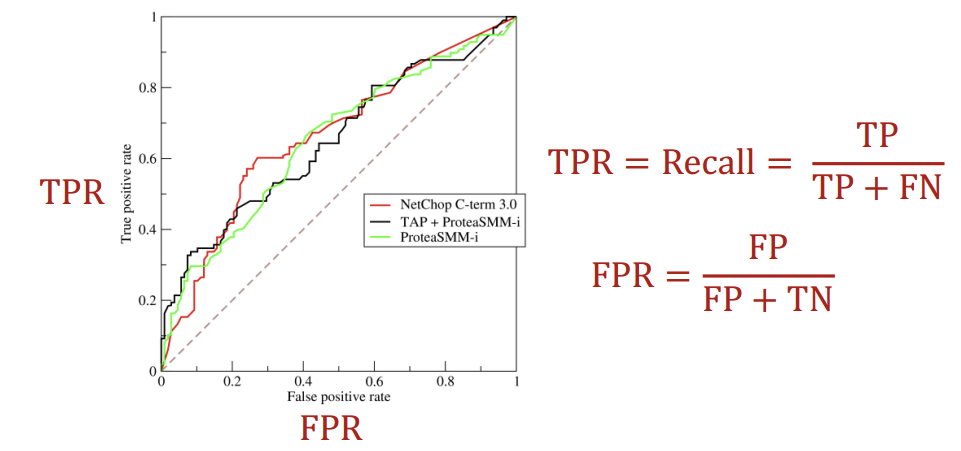
다음은 ROC AUC이다. ROC AUC는 ROC Curve 아래의 면적이라는 뜻이다. ROC Curve는 TPR과 FPR의 tradeoff 비율을 나타낸 그래프로, 랜덤 classification을 하면 직선이 나오고, 정확한 classification 모델일수록 곡선이 점점 좌상단에 가까워진다. 따라서 ROC AUC가 1에 가까울수록 정확도가 높은 모델임을 알 수 있다.

출처, 더 궁금하다면?

Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 8.2 - Training Graph Neural Networks