Embedding Entire Graphs
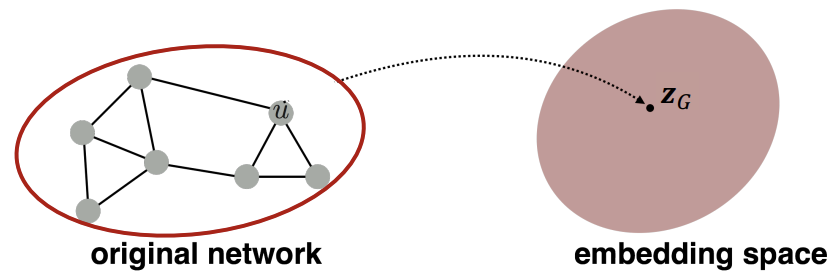
이전 강의에서 Node를 embedding 하는 방법에 대해 배웠다면, 이번 강의에서는 Graph(혹은 Subgraph)를 embedding 하는 방법에 대해 배워보고자 한다.
먼저 가장 단순한 방법으로는, 일반적인 Graph embedding을 한 후, 해당 Graph 내의 Node embedding을 모두 합하는 것이다.
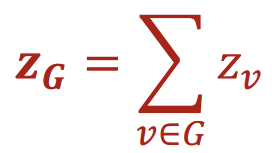
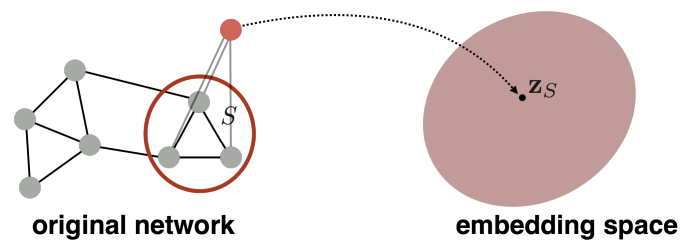
두번째 방법은 첫번째 방법에서 조금 더 발전한 방법으로, embedding 하기 원하는 subgraph를 대표하는 virtual node를 만들고, 그 Node를 embedding space에 올림으로써 subgraph를 embedding space에 올리는 방법이다.
마지막 방법은 아래에서 설명할 Anonymous Walk이다.
Anonymous Walk
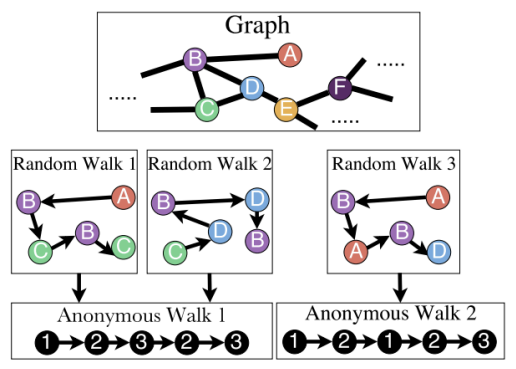
Anonymous walk는 Random walk와 동일하지만, Node를 처음 방문했던 step에 따라 index를 부여받는 식으로 동작한다. 이로인해 서로 다른 Node를 방문하더라도 순서만 일치하면 같은 walk로 간주한다.
이러한 Anonymous walk의 확률 분포를 통해 Graph를 표현할 수 있다. 예를들어, 길이가 3인 walk는 5개가 존재하기 때문에, 각 index에 해당 walk가 될 확률이 들어있는 5차원 vector로 Graph를 표현 가능한 것이다.
이러한 vector를 만들기 위해 Anonymous walk를 sampling 하여 확률 분포를 만들어야한다. 이때 얼마나 많은 random walk를 진행해야하는지는 아래의 수식으로 구할 수 있다.
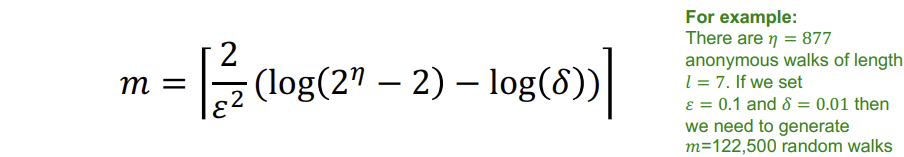
위 공식에 의하면, 길이가 \(l\)인 walk에서 \(\eta\)개의 Anonymous walk가 존재하는 경우, \(\delta\)보다 적은 확률로 \(\varepsilon\)이하의 에러의 분포를 얻기 위해 \(m\)회의 random walk를 sampling 해야한다.
Learn Walk Embeddings
위처럼 각 walk가 나타나는 횟수만으로 표현하는 것보다 anonymous walk \(w_i\)에 대한 embedding \(z_i\)를 학습하는 방법 또한 존재한다. 이러한 embedding들을 전부 합해 Graph 전체의 embedding \(Z_{G} = {z_{i}:i = 1 … \eta}\)를 구하는 것이다.
이를 위해 walk를 embedding 해야한다. 먼저 Node1에 대해 anonymous random walk를 sampling 한 후, \(\Delta\) 크기의 window에서 중복하여 발생하는 walk들을 학습을 통해 예측해야한다. 즉, 앞/뒤 \(\Delta\)개의 walk들을 보고 해당 walk를 예측하는 것이다.
아래는 \(w_t\)를 예측하기 위해 앞/뒤 \(\Delta\)개의 walk를 사용한다는 의미를 담은 수식이다.
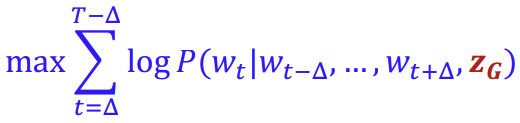
이를 Node u에서 시작하는 길이 l의 T개의 서로 다른 random walk에서 진행하면 다음과 같다.

그러면 Graph에 대한 embedding \(z_G\)를 얻게 된다. 이를 이용해 2강에서 배운 유사도로 예측을 하거나, 이후에 배울 Graph Neural Network에 사용할 수 있다.
아래는 Anonymous walk를 이용한 Graph embedding의 구조이다.
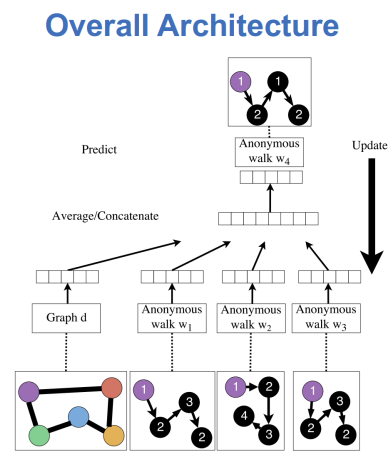
Conclusion
이때까지 배운 Graph embedding의 3가지 방식을 요약하면 다음과 같다.

이후 강의에서는 Hierarchical(계층적인) Embedding을 배우고, 이러한 embedding들을 이용하여 Node Clustering/Classification, Link Prediction, Graph Classification등을 진행할 예정이다.
3강 summary

출처, 더 궁금하다면?
Stanford CS224W: Machine Learning with Graphs | 2021 | Lecture 3.3 - Embedding Entire Graphs